Click here for an english version of this page.







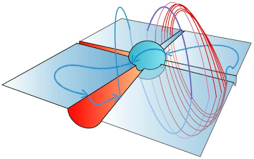
Neste site você encontrará uma série de informações a meu respeito, tais como: disciplinas que estou ministrando ou que já ministrei, orientações de alunos, minhas pesquisas e colaborações, eventos e seminários, minha formação acadêmica e meus interesses científicos. No item Links do menu acima eu selecionei alguns sites que eu julgo conter conteúdo científico/matemático simples e interessante. Mais sugestões de links são bem vindas. Não hesite em me procurar para bater um papo e tomarmos um café! As informações necessárias para me encontrar (email, skype e sala no IMECC) estão na coluna à direita.
Artigos Selecionado
(clique aqui para uma lista completa)
Pedro C. Pereira; Douglas D. Novaes; Murilo R. Cândido
A mechanism for detecting normally hyperbolic invariant tori in differential equations Journal Article
Em: Journal de Mathématiques Pures et Appliquées, vol. 177, não 1, pp. 45, 2023.
@article{PerNovCan23,
title = {A mechanism for detecting normally hyperbolic invariant tori in differential equations},
author = {Pedro C. Pereira and Douglas D. Novaes and Murilo R. Cândido},
url = {https://arxiv.org/abs/2208.10989},
doi = {10.1016/j.matpur.2023.06.008},
year = {2023},
date = {2023-09-01},
urldate = {2023-04-28},
journal = {Journal de Mathématiques Pures et Appliquées},
volume = {177},
number = {1},
pages = {45},
abstract = {Determining the existence of compact invariant manifolds is a central quest in the qualitative theory of differential equations. Singularities, periodic solutions, and invariant tori are examples of such invariant manifolds. A classical and useful result from the averaging theory relates the existence of isolated periodic solutions of non-autonomous periodic differential equations, given in a specific standard form, with the existence of simple singularities of the so-called guiding system, which is an autonomous differential equation given in terms of the average in time of the original non-autonomous one. In this paper, we provide an analogous result for the existence of invariant tori. Namely, we show that a non-autonomous periodic differential equation, given in the standard form, has a normally hyperbolic invariant torus in the extended phase space provided that the guiding system has a hyperbolic limit cycle. We apply this result to show the existence of normally hyperbolic invariant tori in a family of jerk differential equations.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Determining the existence of compact invariant manifolds is a central quest in the qualitative theory of differential equations. Singularities, periodic solutions, and invariant tori are examples of such invariant manifolds. A classical and useful result from the averaging theory relates the existence of isolated periodic solutions of non-autonomous periodic differential equations, given in a specific standard form, with the existence of simple singularities of the so-called guiding system, which is an autonomous differential equation given in terms of the average in time of the original non-autonomous one. In this paper, we provide an analogous result for the existence of invariant tori. Namely, we show that a non-autonomous periodic differential equation, given in the standard form, has a normally hyperbolic invariant torus in the extended phase space provided that the guiding system has a hyperbolic limit cycle. We apply this result to show the existence of normally hyperbolic invariant tori in a family of jerk differential equations.
Douglas D. Novaes; Pedro C. Pereira
Invariant tori via higher order averaging theory: existence, regularity, convergence, stability, and dynamics Journal Article
Em: Mathematische Annalen, vol. 389, pp. 543-590, 2023.
@article{NovPer2022b,
title = {Invariant tori via higher order averaging theory: existence, regularity, convergence, stability, and dynamics},
author = {Douglas D. Novaes and Pedro C. Pereira},
url = {http://arxiv.org/abs/2305.11821},
doi = {10.1007/s00208-023-02654-2},
year = {2023},
date = {2023-06-24},
urldate = {2023-06-24},
journal = {Mathematische Annalen},
volume = {389},
pages = {543-590},
abstract = {Important information about the dynamical structure of a differential system can be revealed by looking into its invariant compact manifolds, such as equilibria, periodic orbits, and invariant tori. This knowledge is significantly increased if asymptotic properties of the trajectories nearby such invariant manifolds can be determined. In this paper, we present a result providing sufficient conditions for the existence of invariant tori in perturbative differential systems. The regularity, convergence, and stability of such tori as well as the dynamics defined on them are also investigated. The conditions are given in terms of their so-called higher order averaged equations. This result is an extension to a wider class of differential systems of theorems due to Krylov, Bogoliubov, Mitropolsky, and Hale.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Important information about the dynamical structure of a differential system can be revealed by looking into its invariant compact manifolds, such as equilibria, periodic orbits, and invariant tori. This knowledge is significantly increased if asymptotic properties of the trajectories nearby such invariant manifolds can be determined. In this paper, we present a result providing sufficient conditions for the existence of invariant tori in perturbative differential systems. The regularity, convergence, and stability of such tori as well as the dynamics defined on them are also investigated. The conditions are given in terms of their so-called higher order averaged equations. This result is an extension to a wider class of differential systems of theorems due to Krylov, Bogoliubov, Mitropolsky, and Hale.
Victoriano Carmona; Fernando Fernández Sánchez; Douglas D. Novaes
Uniform upper bound for the number of limit cycles of planar piecewise linear differential systems with two zones separated by a straight line Journal Article
Em: Applied Mathematics Letters, vol. 137, pp. 108501, 2023.
@article{CarFerNov2022b,
title = {Uniform upper bound for the number of limit cycles of planar piecewise linear differential systems with two zones separated by a straight line},
author = {Victoriano Carmona and Fernando Fernández Sánchez and Douglas D. Novaes},
url = {https://arxiv.org/abs/2210.12125},
doi = {10.1016/j.aml.2022.108501},
year = {2023},
date = {2023-03-01},
journal = {Applied Mathematics Letters},
volume = {137},
pages = {108501},
abstract = {The existence of a uniform upper bound for the maximum number of limit cycles of planar piecewise linear differential systems with two zones separated by a straight line has been subject of interest of hundreds of papers. After more than 30 years of investigation since Lum-Chua's work, it has remained an open question whether this uniform upper bound exists or not. Here, we give a positive answer for this question by establishing the existence of a natural number $L^*leq 8$ for which any planar piecewise linear differential system with two zones separated by a straight line has no more than $L^*$ limit cycles. The proof is obtained by combining a newly developed integral characterization of Poincaré half-maps for linear differential systems with an extension of Khovanskii's theory for investigating the number of intersection points between smooth curves and a particular kind of orbits of vector fields.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
The existence of a uniform upper bound for the maximum number of limit cycles of planar piecewise linear differential systems with two zones separated by a straight line has been subject of interest of hundreds of papers. After more than 30 years of investigation since Lum-Chua's work, it has remained an open question whether this uniform upper bound exists or not. Here, we give a positive answer for this question by establishing the existence of a natural number $L^*leq 8$ for which any planar piecewise linear differential system with two zones separated by a straight line has no more than $L^*$ limit cycles. The proof is obtained by combining a newly developed integral characterization of Poincaré half-maps for linear differential systems with an extension of Khovanskii's theory for investigating the number of intersection points between smooth curves and a particular kind of orbits of vector fields.
Douglas D. Novaes
An averaging result for periodic solutions of Carathéodory differential equations Journal Article
Em: Proceedings of the American Mathematical Society, vol. 150, não 7, pp. 2945-2954, 2022.
@article{Novaes2022,
title = {An averaging result for periodic solutions of Carathéodory differential equations},
author = {Douglas D. Novaes},
url = {http://arxiv.org/abs/2108.01551},
doi = {10.1090/proc/15810},
year = {2022},
date = {2022-04-14},
journal = {Proceedings of the American Mathematical Society},
volume = {150},
number = {7},
pages = {2945-2954},
abstract = {This paper is concerned with the problem of existence of periodic solutions for perturbative Carathéodory differential equations. The main result provides sufficient conditions on the averaged equation that guarantee the existence of periodic solutions. Additional conditions are also provided to ensure the uniform convergence of a periodic solution to a constant function. The proof of the main theorem is mainly based on an abstract continuation result for operator equations.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
This paper is concerned with the problem of existence of periodic solutions for perturbative Carathéodory differential equations. The main result provides sufficient conditions on the averaged equation that guarantee the existence of periodic solutions. Additional conditions are also provided to ensure the uniform convergence of a periodic solution to a constant function. The proof of the main theorem is mainly based on an abstract continuation result for operator equations.
Douglas D. Novaes; Francisco B.G. Silva
Higher order analysis on the existence of periodic solutions in continuous differential equations via degree theory Journal Article
Em: SIAM Journal on Mathematical Analysis, vol. 53, não 2, pp. 2476-2490, 2021.
@article{NovGSilva2021,
title = {Higher order analysis on the existence of periodic solutions in continuous differential equations via degree theory},
author = {Douglas D. Novaes and Francisco B.G. Silva},
url = {http://arxiv.org/abs/2006.10799},
year = {2021},
date = {2021-01-05},
urldate = {2021-01-05},
journal = {SIAM Journal on Mathematical Analysis},
volume = {53},
number = {2},
pages = {2476-2490},
abstract = {Recently, the higher order averaging method for studying periodic solutions of both Lipschitz differential equations and discontinuous piecewise smooth differential equations was developed in terms of the Brouwer degree theory. Between the Lipschitz and the discontinuous piecewise smooth differential equations, there is a huge class of differential equations lacking in a higher order analysis on the existence of periodic solutions, namely the class of continuous non-Lipschitz differential equations. In this paper, based on the degree theory for operator equations, we perform a higher order analysis of continuous perturbed differential equations and derive sufficient conditions for the existence and uniform convergence of periodic solutions for such systems. We apply our results to study continuous non-Lipschitz higher order perturbations of a harmonic oscillator.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Recently, the higher order averaging method for studying periodic solutions of both Lipschitz differential equations and discontinuous piecewise smooth differential equations was developed in terms of the Brouwer degree theory. Between the Lipschitz and the discontinuous piecewise smooth differential equations, there is a huge class of differential equations lacking in a higher order analysis on the existence of periodic solutions, namely the class of continuous non-Lipschitz differential equations. In this paper, based on the degree theory for operator equations, we perform a higher order analysis of continuous perturbed differential equations and derive sufficient conditions for the existence and uniform convergence of periodic solutions for such systems. We apply our results to study continuous non-Lipschitz higher order perturbations of a harmonic oscillator.
Douglas D. Novaes; Marco A. Teixeira
Shilnikov problem in Filippov dynamical systems Journal Article
Em: Chaos, vol. 29, pp. 063110, 2019.
@article{NovTei2019,
title = {Shilnikov problem in Filippov dynamical systems},
author = {Douglas D. Novaes and Marco A. Teixeira},
url = {https://doi.org/10.1063/1.5093067
http://arxiv.org/abs/1504.02425},
doi = {10.1063/1.5093067},
year = {2019},
date = {2019-06-20},
journal = {Chaos},
volume = {29},
pages = {063110},
abstract = {In this paper we introduce the concept of sliding Shilnikov orbits for $3$D Filippov systems. In short, such an orbit is a piecewise smooth closed curve, composed by Filippov trajectories, which slides on the switching surface and connects a Filippov equilibrium to itself, namely a pseudo saddle-focus. A version of the Shilnikov's Theorem is provided for such systems. Particularly, we show that sliding Shilnikov orbits occur in generic one-parameter families of Filippov systems, and that arbitrarily close to a sliding Shilnikov orbit there exist countably infinitely many sliding periodic orbits. Here, no additional Shilnikov-like assumption is needed in order to get this last result. In addition, we show the existence of sliding Shilnikov orbits in discontinuous piecewise linear differential systems. As far as we know, the examples of Fillippov systems provided in this paper are the first exhibiting such a sliding phenomenon.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
In this paper we introduce the concept of sliding Shilnikov orbits for $3$D Filippov systems. In short, such an orbit is a piecewise smooth closed curve, composed by Filippov trajectories, which slides on the switching surface and connects a Filippov equilibrium to itself, namely a pseudo saddle-focus. A version of the Shilnikov's Theorem is provided for such systems. Particularly, we show that sliding Shilnikov orbits occur in generic one-parameter families of Filippov systems, and that arbitrarily close to a sliding Shilnikov orbit there exist countably infinitely many sliding periodic orbits. Here, no additional Shilnikov-like assumption is needed in order to get this last result. In addition, we show the existence of sliding Shilnikov orbits in discontinuous piecewise linear differential systems. As far as we know, the examples of Fillippov systems provided in this paper are the first exhibiting such a sliding phenomenon.
Douglas D. Novaes; Joan Torregrosa
On the extended Chebyshev systems with positive accuracy Journal Article
Em: J. Math. Anal. Appl., vol. 488, não 1, pp. 171-186, 2017.
@article{NovTor2017,
title = {On the extended Chebyshev systems with positive accuracy},
author = {Douglas D. Novaes and Joan Torregrosa},
url = {http://dx.doi.org/10.1016/j.jmaa.2016.10.076},
doi = {10.1016/j.jmaa.2016.10.076},
year = {2017},
date = {2017-04-01},
urldate = {2017-04-01},
journal = {J. Math. Anal. Appl.},
volume = {488},
number = {1},
pages = {171-186},
abstract = {A classical necessary condition for an ordered set of n+1 functions F to be an ECT-system in a closed interval is that all the Wronskians do not vanish. With this condition all the elements of Span(F) have at most n zeros taking into account the multiplicity. Here the problem of bounding the number of zeros of Span(F) is considered as well as the effectiveness of the upper bound when some Wronskians vanish. For this case we also study the possible configurations of zeros that can be realized by elements of Span(F). An application to counting the number of isolated periodic orbits for a family of nonsmooth systems is done.
},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
A classical necessary condition for an ordered set of n+1 functions F to be an ECT-system in a closed interval is that all the Wronskians do not vanish. With this condition all the elements of Span(F) have at most n zeros taking into account the multiplicity. Here the problem of bounding the number of zeros of Span(F) is considered as well as the effectiveness of the upper bound when some Wronskians vanish. For this case we also study the possible configurations of zeros that can be realized by elements of Span(F). An application to counting the number of isolated periodic orbits for a family of nonsmooth systems is done.
Douglas D. Novaes; Gabriel Ponce; Régis Varão
Chaos induced by sliding phenomena in Filippov systems Journal Article
Em: Journal of Dynamics and Differential Equations, pp. 1-15, 2017.
@article{NovPonVar2017,
title = {Chaos induced by sliding phenomena in Filippov systems},
author = {Douglas D. Novaes and Gabriel Ponce and Régis Varão},
url = {http://dx.doi.org/10.1007/s10884-017-9580-8},
doi = {10.1007/s10884-017-9580-8},
year = {2017},
date = {2017-02-16},
journal = {Journal of Dynamics and Differential Equations},
pages = {1-15},
abstract = {In this paper we provide a full topological and ergodic description of the dynamics of Filippov systems nearby a sliding Shilnikov orbit G. More specifically we prove that the first return map, defined nearby G, is topologically conjugate to a Bernoulli shift with infinite topological entropy. In particular, we see that for each natural number m it has infinitely many periodic points with period m.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
In this paper we provide a full topological and ergodic description of the dynamics of Filippov systems nearby a sliding Shilnikov orbit G. More specifically we prove that the first return map, defined nearby G, is topologically conjugate to a Bernoulli shift with infinite topological entropy. In particular, we see that for each natural number m it has infinitely many periodic points with period m.
Jaume Llibre; Ana C. Mereu; Douglas D. Novaes
Averaging theory for discontinuous piecewise differential systems Journal Article
Em: Journal of Differential Equations, vol. 258, não 11, pp. 4007 - 4032, 2015.
@article{LliMerNovJDF2015,
title = {Averaging theory for discontinuous piecewise differential systems},
author = {Jaume Llibre and Ana C. Mereu and Douglas D. Novaes},
url = {http://dx.doi.org/10.1016/j.jde.2015.01.022},
doi = {10.1016/j.jde.2015.01.022},
year = {2015},
date = {2015-01-01},
journal = {Journal of Differential Equations},
volume = {258},
number = {11},
pages = {4007 - 4032},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Douglas D. Novaes; Mike R. Jeffrey
Regularization of hidden dynamics in piecewise smooth flows Journal Article
Em: Journal of Differential Equations, vol. 259, não 9, pp. 4615 - 4633, 2015.
@article{NovJefJDE2015,
title = {Regularization of hidden dynamics in piecewise smooth flows},
author = {Douglas D. Novaes and Mike R. Jeffrey},
url = {http://dx.doi.org/10.1016/j.jde.2015.06.005},
doi = {10.1016/j.jde.2015.06.005},
year = {2015},
date = {2015-01-01},
journal = {Journal of Differential Equations},
volume = {259},
number = {9},
pages = {4615 - 4633},
abstract = {This paper studies the equivalence between differentiable and non-differentiable dynamics in Rn . Filippov's theory of discontinuous differential equations allows us to find flow solutions of dynamical systems whose vector fields undergo switches at thresholds in phase space. The canonical convex combination at the discontinuity is only the linear part of a nonlinear combination that more fully explores Filippov's most general problem: the differential inclusion. Here we show how recent work relating discontinuous systems to singular limits of continuous (or regularized) systems extends to nonlinear combinations. We show that if sliding occurs in a discontinuous systems, there exists a differentiable slow–fast system with equivalent slow invariant dynamics. We also show the corresponding result for the pinching method, a converse to regularization which approximates a smooth system by a discontinuous one.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
This paper studies the equivalence between differentiable and non-differentiable dynamics in Rn . Filippov's theory of discontinuous differential equations allows us to find flow solutions of dynamical systems whose vector fields undergo switches at thresholds in phase space. The canonical convex combination at the discontinuity is only the linear part of a nonlinear combination that more fully explores Filippov's most general problem: the differential inclusion. Here we show how recent work relating discontinuous systems to singular limits of continuous (or regularized) systems extends to nonlinear combinations. We show that if sliding occurs in a discontinuous systems, there exists a differentiable slow–fast system with equivalent slow invariant dynamics. We also show the corresponding result for the pinching method, a converse to regularization which approximates a smooth system by a discontinuous one.
Jaume Llibre; Douglas D. Novaes; Marco A. Teixeira
Higher order averaging theory for finding periodic solutions via Brouwer degree Journal Article
Em: Nonlinearity, vol. 27, não 3, pp. 563, 2014.
@article{LliNovTeiN2014,
title = {Higher order averaging theory for finding periodic solutions via Brouwer degree},
author = {Jaume Llibre and Douglas D. Novaes and Marco A. Teixeira},
url = {http://dx.doi.org/10.1088/0951-7715/27/3/563},
doi = {10.1088/0951-7715/27/3/563},
year = {2014},
date = {2014-01-01},
journal = {Nonlinearity},
volume = {27},
number = {3},
pages = {563},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Formação
Livre-Docente em Matemática, 2019, UNICAMP.
Pós-Doutorado, 2015 e 2016, UNICAMP e UAB.
Doutor em Matemática, 2015, UNICAMP (download da tese).
Estágio de Pesquisa no Exterior, 2014, UAB, Barcelona-Espanha.
Mestre em Matemática, 2012, UNICAMP (link da dissertação).
Licenciatura em Matemática, 2010, UNICAMP.
Prêmios
Menção Honrosa – Prêmio Carlos Teobaldo Gutierrez Vidalon 2016.
Menção Honrosa – XVIII Congresso Interno de Iniciação Científica da UNICAMP.
Interesses Científicos
(clique aqui para mais detalhes)
- Averaging theory, Melnikov method, Lyapunov-Schmidit reduction, Relaxation Oscillation theory, and other tools to study and detect invariant sets.
- Chebyshev systems with positive accuracy and their applications in dynamics.
- Hidden dynamics, regularization and pinching of Filippov and non Filippov systems.
- Singular perturbation problems and their relation with regularization of piecewise smooth vector fields.
- Typical cycles and global dynamics of piecewise smooth vector fields.
- Sliding dynamics and chaos.
- Invariant measures for piecewise smooth vector fields.
- Differential Inclusions.
No arquivo a seguir você encontrará alguns comentários elaborados pelo Prof. Marco Antonio Teixeira sobre uma das linhas de pesquisa na qual estou inserido: Non-smooth dynamical system – Reflections and Guidelines.