- Averaging theory, Melnikov method, Lyapunov-Schmidit reduction, Relaxation Oscillation theory, and other tools to study and detect invariant sets.
- Chebyshev systems with positive accuracy and their applications in dynamics.
- Hidden dynamics, regularization and pinching of Filippov and non Filippov systems.
- Singular perturbation problems and their relation with regularization of piecewise smooth vector fields.
- Typical cycles and global dynamics of piecewise smooth vector fields.
- Sliding dynamics and chaos.
- Invariant measures for piecewise smooth vector fields.
- Differential Inclusions.
Sala
IMECC 342 - 3ºandar
Contato
email: ddnovaes@unicamp.br
skype: ddnovaes
phone: +55 19 3521-6035Endereço
Rua Sérgio Buarque de Holanda, 651,
Cidade Universitária, 13083-859,
Campinas, São Paulo, Brasil._________________________
Grupo de Pesquisa em Sistemas Dinâmicos do IMECC
_________________________
Instituto de Matemática, Estatística e Computação Científica
_________________________
Universidade Estadual de Campinas
_________________________
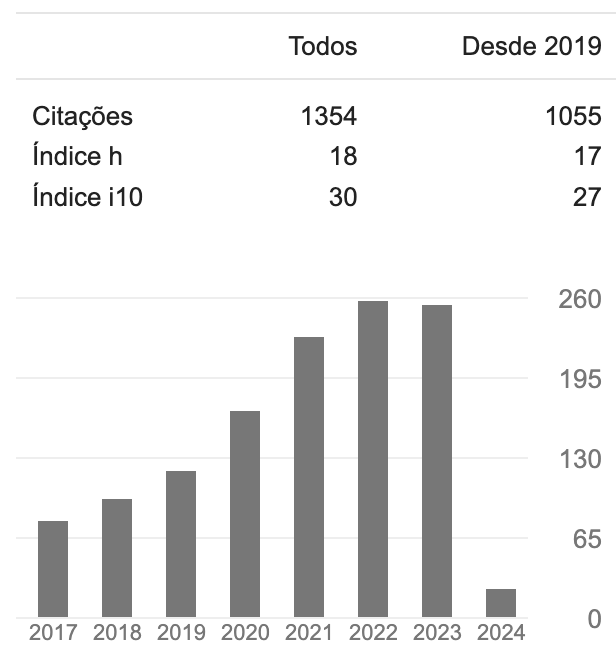
Citações Google Acadêmico