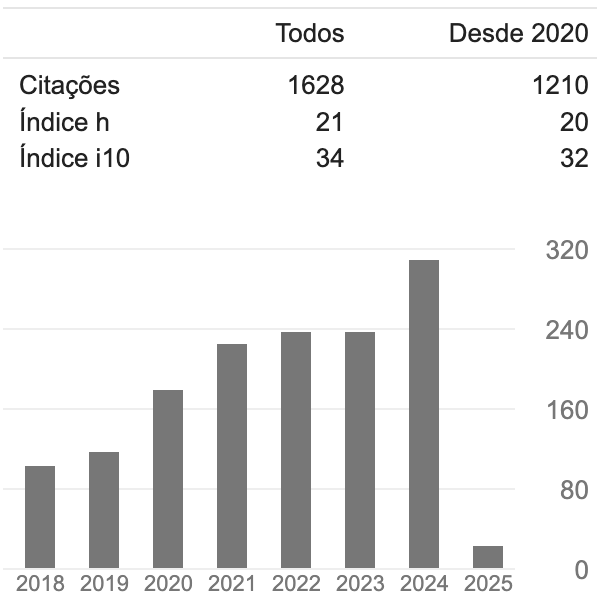
2025
Douglas D. Novaes; Leandro A. Silva
Unveiling the cyclicity of monodromic tangential singularities: Insights beyond the pseudo-Hopf bifurcation Journal Article
Em: SIAM Journal on Applied Dynamical Systems , vol. 24, iss. 1, pp. 165-186, 2025.
@article{NovaesLSilva2025,
title = {Unveiling the cyclicity of monodromic tangential singularities: Insights beyond the pseudo-Hopf bifurcation},
author = {Douglas D. Novaes and Leandro A. Silva},
url = {https://arxiv.org/abs/2303.06027},
doi = {10.1137/24M1668329},
year = {2025},
date = {2025-01-09},
urldate = {2025-01-09},
journal = {SIAM Journal on Applied Dynamical Systems },
volume = {24},
issue = {1},
pages = {165-186},
abstract = {The cyclicity problem, crucial in analyzing planar vector fields, consists in estimating the number of limit cycles emanating from monodromic singularities. Traditionally, this estimation relies on Lyapunov coefficients. However, in nonsmooth systems, besides the limit cycles bifurcating by varying the Lyapunov coefficients, monodromic singularities on the switching curve can always be split apart yielding, under suitable conditions, a sliding region and an additional limit cycle surrounding it. This bifurcation phenomenon, known as pseudo-Hopf bifurcation, has enhanced lower-bound cyclicity estimations for monodromic singularities in Filippov systems. In this study, we push beyond the pseudo-Hopf bifurcation, demonstrating that the destruction of (2k,2k)-monodromic tangential singularities yields at least k limit cycles surrounding sliding segments. This new bifurcation phenomenon expands our understanding of limit cycle bifurcations in nonsmooth systems and, in addition to the theoretical significance, has practical relevance in various applied models involving switches and abrupt processes.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
2024
Douglas D. Novaes; Pedro C. Pereira
A version of Hilbert's 16th Problem for 3D polynomial vector fields: counting isolated invariant tori Journal Article
Em: Mathematische Nachrichten, pp. 1-9, 2024.
@article{NovPer2024,
title = {A version of Hilbert's 16th Problem for 3D polynomial vector fields: counting isolated invariant tori},
author = {Douglas D. Novaes and Pedro C. Pereira},
url = {https://arxiv.org/abs/2212.12006},
doi = {10.1002/mana.202300568},
year = {2024},
date = {2024-12-30},
urldate = {2024-12-30},
journal = {Mathematische Nachrichten},
pages = {1-9},
abstract = {Hilbert's 16th Problem, about the maximum number of limit cycles of planar polynomial vector fields of a given degree $m$, has been one of the most important driving forces for new developments in the qualitative theory of vector fields. Increasing the dimension, one cannot expect the existence of a finite upper bound for the number of limit cycles of, for instance, $3$D polynomial vector fields of a given degree $m$. Here, as an extension of such a problem in the $3$D space, we investigate the number of isolated invariant tori in $3$D polynomial vector fields. In this context, given a natural number $m$, we denote by $N(m)$ the upper bound for the number of isolated invariant tori of $3$D polynomial vector fields of degree $m$. Based on a recently developed averaging method for detecting invariant tori, our first main result provides a mechanism for constructing $3$D differential vector fields with a number $H$ of normally hyperbolic invariant tori from a given planar differential vector field with $H$ hyperbolic limit cycles. The strength of our mechanism in studying the number $N(m)$ lies in the fact that the constructed $3$D differential vector field is polynomial provided that the given planar differential vector field is polynomial. Accordingly, our second main result establishes a lower bound for $N(m)$ in terms of lower bounds for the number of hyperbolic limit cycles of planar polynomial vector fields of degree $[m/2]-1$. Based on this last result, we apply a methodology due to Christopher & Lloyd to show that $N(m)$ grows as fast as $m^3/128$. Finally, the above-mentioned problem is also formulated for higher dimensional polynomial vector fields.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Joyce A. Casimiro; Ricardo M. Martins; Douglas D. Novaes
Poincaré-Hopf Theorem for Filippov vector fields on 2 dimensional manifolds Journal Article
Em: Communications on Pure and Applied Analysis, vol. 23, iss. 11, pp. 1770-1796, 2024.
@article{CasMarNov24,
title = {Poincaré-Hopf Theorem for Filippov vector fields on 2 dimensional manifolds},
author = {Joyce A. Casimiro and Ricardo M. Martins and Douglas D. Novaes},
url = {https://arxiv.org/abs/2303.04316},
doi = {10.3934/cpaa.2024066},
year = {2024},
date = {2024-11-01},
urldate = {2024-11-01},
journal = {Communications on Pure and Applied Analysis},
volume = {23},
issue = {11},
pages = {1770-1796},
abstract = {The Poincaré–Hopf Theorem relates the Euler characteristic of a 2-dimensional compact manifold to the local behavior of smooth vector fields defined on it. However, despite the importance of Filippov vector fields, concerning both their theoretical and applied aspects, until now, it was not known whether this theorem extends to Filippov vector fields. In this paper, we demonstrate that the Poincaré–Hopf Theorem applies to Filippov vector fields defined on 2-dimensional compact manifolds with smooth switching manifolds. As a result, we establish a variant of the Hairy Ball Theorem, asserting that ``any Filippov vector field on a sphere with smooth switching manifolds must have at least one singularity (in the Filippov sense) with positive index''. This extension is achieved by introducing a new index definition that includes the singularities of Filippov vector fields, such as pseudo-equilibria and tangential singularities. Our work extends the classical index definition for singularities of smooth vector fields to encompass those of Filippov vector fields with smooth switching manifolds. This extension is based on an invariance property under a regularization process, allowing us to establish all classical index properties. We also compute the indices of all generic $Sigma$-singularities and some codimension-1 $Sigma$-singularities, including fold-fold tangential singularities, regular-cusp tangential singularities, and saddle-node pseudo-equilibria.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Matheus G. C. Cunha; Douglas D. Novaes; Gabriel Ponce
On the Hausdorff dimension and Cantor set structure of sliding Shilnikov invariant sets Journal Article
Em: Nonlinearity, vol. 37, não 125023, 2024.
@article{CunNovPon2024,
title = {On the Hausdorff dimension and Cantor set structure of sliding Shilnikov invariant sets},
author = {Matheus G. C. Cunha and Douglas D. Novaes and Gabriel Ponce},
url = {https://arxiv.org/abs/2312.10720},
doi = {10.1088/1361-6544/ad8d9c},
year = {2024},
date = {2024-10-31},
urldate = {2024-10-31},
journal = {Nonlinearity},
volume = {37},
number = {125023},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Douglas D. Novaes
Addendum to Higher order stroboscopic averaged functions: a general relationship with Melnikov functions Journal Article
Em: Electron. J. Qual. Theory Differ. Equ., vol. 2024, iss. 64, não 1, pp. 3, 2024.
@article{Novaes2024,
title = {Addendum to Higher order stroboscopic averaged functions: a general relationship with Melnikov functions},
author = {Douglas D. Novaes},
url = {https://arxiv.org/abs/2409.05912},
doi = {10.14232/ejqtde.2024.1.64},
year = {2024},
date = {2024-10-13},
urldate = {2024-10-13},
journal = {Electron. J. Qual. Theory Differ. Equ.},
volume = {2024},
number = {1},
issue = {64},
pages = {3},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Tiago de Carvalho; Douglas D. Novaes; Durval J. Tonon
Sliding mode on tangential sets of Filippov systems Journal Article
Em: J Nonlinear Sci., vol. 34, não 70, 2024.
@article{CarNovTon2021,
title = {Sliding mode on tangential sets of Filippov systems},
author = {Tiago de Carvalho and Douglas D. Novaes and Durval J. Tonon},
url = {https://arxiv.org/abs/2111.12377},
doi = {10.1007/s00332-024-10052-4},
year = {2024},
date = {2024-06-09},
urldate = {2024-06-09},
journal = {J Nonlinear Sci.},
volume = {34},
number = {70},
abstract = {We consider piecewise smooth vector fields $Z=(Z_+, Z_-)$ defined in $R^n$ where both vector fields are tangent to the switching manifold $Sigma$ along a manifold $M$. Our main purpose is to study the existence of an invariant vector field defined on $M$, that we call {it tangential sliding vector field}. We provide necessary and sufficient conditions under $Z$ to characterize the existence of this vector field. Considering a regularization process, we proved that this tangential sliding vector field is topological equivalent to an invariant dynamics under the slow manifold. Besides then, at the end of the work we apply the results in a system that governs the intermittent treatment of HIV.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Douglas D. Novaes; Luan V. M. F. Silva
A Melnikov analysis on a family of second order discontinuous differential equations Journal Article
Em: São Paulo J. Math. Sci., vol. 18, pp. 1486-1504, 2024.
@article{NovLSilva2023b,
title = {A Melnikov analysis on a family of second order discontinuous differential equations},
author = {Douglas D. Novaes and Luan V. M. F. Silva},
url = {https://arxiv.org/abs/2312.02738},
doi = {10.1007/s40863-024-00436-5},
year = {2024},
date = {2024-06-03},
urldate = {2024-06-03},
journal = {São Paulo J. Math. Sci.},
volume = {18},
pages = {1486-1504},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Douglas D. Novaes; Pedro C. Pereira
On the periodic and antiperiodic aspects of the Floquet normal form Journal Article
Em: Bulletin des Sciences Mathématiques, vol. 190, pp. 103378, 2024.
@article{NovPer2024,
title = {On the periodic and antiperiodic aspects of the Floquet normal form},
author = {Douglas D. Novaes and Pedro C. Pereira},
url = {https://arxiv.org/abs/2312.05608},
doi = {10.1016/j.bulsci.2023.103378},
year = {2024},
date = {2024-02-01},
urldate = {2024-02-01},
journal = {Bulletin des Sciences Mathématiques},
volume = {190},
pages = {103378},
abstract = {Floquet's Theorem is a celebrated result in the theory of ordinary differential equations. Essentially, the theorem states that, when studying a linear differential system with T-periodic coefficients, we can apply a, possibly complex, T-periodic change of variables that transforms it into a linear system with constant coefficients. In this paper, we explore further the question of the nature of this change of variables. We state necessary and sufficient conditions for it to be real and T-periodic. Failing those conditions, we prove that we can still find a real change of variables that is “partially” T-periodic and “partially” T-antiperiodic. We also present applications of this new form of Floquet's Theorem to the study of the behavior of solutions of nonlinear differential systems near periodic orbits.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Douglas D. Novaes; Luan V. M. F. Silva
Invariant tori and boundedness of solutions of non-smooth oscillators with Lebesgue integrable forcing term Journal Article
Em: Zeitschrift für angewandte Mathematik und Physik, vol. 75, iss. 10, não 1, pp. 13, 2024.
@article{NovFSilva2024,
title = {Invariant tori and boundedness of solutions of non-smooth oscillators with Lebesgue integrable forcing term},
author = {Douglas D. Novaes and Luan V. M. F. Silva},
url = {https://arxiv.org/abs/2305.13457},
doi = {10.1007/s00033-023-02152-0},
year = {2024},
date = {2024-01-11},
urldate = {2024-01-11},
journal = {Zeitschrift für angewandte Mathematik und Physik},
volume = {75},
number = {1},
issue = {10},
pages = {13},
abstract = {Since Littlewood works in the 1960's, the boundedness of solutions of Duffing-type equations $ddot{x}+g(x)=p(t)$ has been extensively investigated. More recently, some researches have focused on the family of non-smooth forced oscillators $ ddot{x}+sgn(x)=p(t)$, mainly because it represents a simple limit scenario of Duffing-type equations for when $g$ is bounded. Here, we provide a simple proof for the boundedness of solutions of the non-smooth forced oscillator in the case that the forcing term $p(t)$ is a $T$-periodic Lebesgue integrable function with vanishing average. We reach this result by constructing a sequence of invariant tori whose union of their interiors covers all the $(t,x,dot x)$-space, $(t,x,dot x)in s^1timesR^2$.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
2023
Kamila S. Andrade; Otávio M.L. Gomide; Douglas D. Novaes; Marco A. Teixeira
Bifurcation Diagrams of Global Connections in Filippov Systems Journal Article
Em: Nonlinear Analysis: Hybrid Systems, vol. 50, pp. 101397, 2023.
@article{AndGomNov2023,
title = {Bifurcation Diagrams of Global Connections in Filippov Systems},
author = {Kamila S. Andrade and Otávio M.L. Gomide and Douglas D. Novaes and Marco A. Teixeira },
url = {http://arxiv.org/abs/1905.11950},
doi = {10.1016/j.nahs.2023.101397},
year = {2023},
date = {2023-11-01},
urldate = {2023-11-01},
journal = {Nonlinear Analysis: Hybrid Systems},
volume = {50},
pages = {101397},
abstract = {In this paper, we are concerned about the qualitative behaviour of planar Filippov systems around some typical minimal sets, namely, polycycles. In the smooth context, a polycycle is a simple closed curve composed by a collection of singularities and regular orbits, inducing a first return map. Here, this concept is extended to Filippov systems by allowing typical singularities lying on the switching manifold. Our main goal consists in developing a method to investigate the unfolding of polycycles in Filippov systems. In addition, we applied this method to describe bifurcation diagrams of Filippov systems around certain polycycles. },
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Cláudio Pessoa; Ronísio Ribeiro; Douglas D. Novaes; Márcio R. A. Gouveia; Rodrigo Euzébio
On cyclicity in discontinuous piecewise linear near-hamiltonian differential systems with three zones having a saddle in the central one Journal Article
Em: Nonlinear Dynamics, 2023.
@article{EuzGouNovPesRib2023,
title = {On cyclicity in discontinuous piecewise linear near-hamiltonian differential systems with three zones having a saddle in the central one},
author = {Cláudio Pessoa and Ronísio Ribeiro and Douglas D. Novaes and Márcio R. A. Gouveia and Rodrigo Euzébio},
url = {https://arxiv.org/abs/2212.00828},
year = {2023},
date = {2023-10-04},
urldate = {2022-12-16},
journal = {Nonlinear Dynamics},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Pedro C. Pereira; Douglas D. Novaes; Murilo R. Cândido
A mechanism for detecting normally hyperbolic invariant tori in differential equations Journal Article
Em: Journal de Mathématiques Pures et Appliquées, vol. 177, não 1, pp. 45, 2023.
@article{PerNovCan23,
title = {A mechanism for detecting normally hyperbolic invariant tori in differential equations},
author = {Pedro C. Pereira and Douglas D. Novaes and Murilo R. Cândido},
url = {https://arxiv.org/abs/2208.10989},
doi = {10.1016/j.matpur.2023.06.008},
year = {2023},
date = {2023-09-01},
urldate = {2023-04-28},
journal = {Journal de Mathématiques Pures et Appliquées},
volume = {177},
number = {1},
pages = {45},
abstract = {Determining the existence of compact invariant manifolds is a central quest in the qualitative theory of differential equations. Singularities, periodic solutions, and invariant tori are examples of such invariant manifolds. A classical and useful result from the averaging theory relates the existence of isolated periodic solutions of non-autonomous periodic differential equations, given in a specific standard form, with the existence of simple singularities of the so-called guiding system, which is an autonomous differential equation given in terms of the average in time of the original non-autonomous one. In this paper, we provide an analogous result for the existence of invariant tori. Namely, we show that a non-autonomous periodic differential equation, given in the standard form, has a normally hyperbolic invariant torus in the extended phase space provided that the guiding system has a hyperbolic limit cycle. We apply this result to show the existence of normally hyperbolic invariant tori in a family of jerk differential equations.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Victoriano Carmona; Fernando Fernández Sánchez; Douglas D. Novaes
Uniqueness and stability of limit cycles in planar piecewise linear differential systems without sliding region Journal Article
Em: Communications in Nonlinear Science and Numerical Simulation, vol. 123, pp. 107257, 2023.
@article{CarFerNov2023b,
title = {Uniqueness and stability of limit cycles in planar piecewise linear differential systems without sliding region},
author = {Victoriano Carmona and Fernando Fernández Sánchez and Douglas D. Novaes},
url = {https://arxiv.org/abs/2207.14634},
doi = {10.1016/j.cnsns.2023.107257},
year = {2023},
date = {2023-08-01},
urldate = {2023-08-01},
journal = {Communications in Nonlinear Science and Numerical Simulation},
volume = {123},
pages = {107257},
abstract = {In this paper, we consider the family of planar piecewise linear differential systems with two zones separated by a straight line without sliding regions, that is, differential systems whose flow transversally crosses the switching line except for at most one point. In the research literature, many papers deal with the problem of determining the maximum number of limit cycles that these differential systems can have. This problem has been usually approached via large case-by-case analyses which distinguish the many different possibilities for the spectra of the matrices of the differential systems. Here, by using a novel integral characterization of Poincaré half-maps, we prove, without unnecessary distinctions of matrix spectra, that the optimal uniform upper bound for the number of limit cycles of these differential systems is one. In addition, it is proven that this limit cycle, if it exists, is hyperbolic and its stability is determined by a simple condition in terms of the parameters of the system. As a byproduct of our analysis, a condition for the existence of the limit cycle is also derived.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Victoriano Carmona; Fernando Fernández Sánchez; Douglas D. Novaes
A succinct characterization of period annuli in planar piecewise linear differential systems with a straight line of nonsmoothness Journal Article
Em: Journal of Nonlinear Science, vol. 33, iss. 5, não 88, pp. 1-13, 2023.
@article{CarFerNov2022c,
title = {A succinct characterization of period annuli in planar piecewise linear differential systems with a straight line of nonsmoothness},
author = {Victoriano Carmona and Fernando Fernández Sánchez and Douglas D. Novaes},
url = {http://arxiv.org/abs/2212.09063},
doi = {10.1007/s00332-023-09947-5},
year = {2023},
date = {2023-07-17},
urldate = {2023-07-17},
journal = {Journal of Nonlinear Science},
volume = {33},
number = {88},
issue = {5},
pages = {1-13},
abstract = {We close the problem of the existence of period annuli in planar piecewise linear differential systems with a straight line of nonsmoothness. In fact, a characterization for the existence of such objects is provided by means of a few basic operations on the parameters.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Jaume Llibre; Douglas D. Novaes; Claudia Valls
Existence of a cylinder foliated by periodic orbits in the generalized Chazy differential equation Journal Article
Em: Chaos, vol. 33, iss. 7, pp. 073104, 2023.
@article{LliNovVal23,
title = {Existence of a cylinder foliated by periodic orbits in the generalized Chazy differential equation},
author = {Jaume Llibre and Douglas D. Novaes and Claudia Valls},
url = {https://arxiv.org/abs/2307.00087},
doi = {10.1063/5.0138309},
year = {2023},
date = {2023-07-05},
urldate = {2023-07-05},
journal = {Chaos},
volume = {33},
issue = {7},
pages = {073104},
abstract = {The generalized Chazy differential equation corresponds to the following $2$-parameter family of differential equations
$$
dddot x+|x|^q ddot x+dfrac{k |x|^q}{x}dot x^2=0,
$$
which has its regularity varying with $q$ , a positive integer. Indeed, for $q=1$ it is discontinuous on the straight line $x=0$, whereas for $q$ a positive even integer it is polynomial, and for $q>1$ a positive odd integer it is continuous but not differentiable on the straight line $x=0$. In 1999, the existence of periodic solutions in the generalized Chazy differential equation was numerically observed for $q=2$ and $k=3$. In this paper, we prove analytically the existence of such periodic solutions. Our strategy allows to establish sufficient conditions ensuring that the generalized Chazy differential equation, for $k=q+1$ and any positive integer $q$ , has actually an invariant topological cylinder foliated by periodic solutions in the $(x,dot x,ddot x)$-space . In order to set forth the bases of our approach, we start by considering $q=1,2,3$, which are representatives of the different classes of regularity. For an arbitrary positive integer $q$ , an algorithm is provided for checking the sufficient conditions for the existence of such invariant cylinder, which we conjecture that always exists. The algorithm was successfully applied up to $q=100$.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
$$
dddot x+|x|^q ddot x+dfrac{k |x|^q}{x}dot x^2=0,
$$
which has its regularity varying with $q$ , a positive integer. Indeed, for $q=1$ it is discontinuous on the straight line $x=0$, whereas for $q$ a positive even integer it is polynomial, and for $q>1$ a positive odd integer it is continuous but not differentiable on the straight line $x=0$. In 1999, the existence of periodic solutions in the generalized Chazy differential equation was numerically observed for $q=2$ and $k=3$. In this paper, we prove analytically the existence of such periodic solutions. Our strategy allows to establish sufficient conditions ensuring that the generalized Chazy differential equation, for $k=q+1$ and any positive integer $q$ , has actually an invariant topological cylinder foliated by periodic solutions in the $(x,dot x,ddot x)$-space . In order to set forth the bases of our approach, we start by considering $q=1,2,3$, which are representatives of the different classes of regularity. For an arbitrary positive integer $q$ , an algorithm is provided for checking the sufficient conditions for the existence of such invariant cylinder, which we conjecture that always exists. The algorithm was successfully applied up to $q=100$.
Douglas D. Novaes; Pedro C. Pereira
Invariant tori via higher order averaging theory: existence, regularity, convergence, stability, and dynamics Journal Article
Em: Mathematische Annalen, vol. 389, pp. 543-590, 2023.
@article{NovPer2022b,
title = {Invariant tori via higher order averaging theory: existence, regularity, convergence, stability, and dynamics},
author = {Douglas D. Novaes and Pedro C. Pereira},
url = {http://arxiv.org/abs/2305.11821},
doi = {10.1007/s00208-023-02654-2},
year = {2023},
date = {2023-06-24},
urldate = {2023-06-24},
journal = {Mathematische Annalen},
volume = {389},
pages = {543-590},
abstract = {Important information about the dynamical structure of a differential system can be revealed by looking into its invariant compact manifolds, such as equilibria, periodic orbits, and invariant tori. This knowledge is significantly increased if asymptotic properties of the trajectories nearby such invariant manifolds can be determined. In this paper, we present a result providing sufficient conditions for the existence of invariant tori in perturbative differential systems. The regularity, convergence, and stability of such tori as well as the dynamics defined on them are also investigated. The conditions are given in terms of their so-called higher order averaged equations. This result is an extension to a wider class of differential systems of theorems due to Krylov, Bogoliubov, Mitropolsky, and Hale.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Victoriano Carmona; Fernando Fernández Sánchez; Eli García-Medina; Douglas D. Novaes
Properties of Poincaré half-maps for planar linear systems and some direct applications to periodic orbits of piecewise systems Journal Article
Em: Electronic Journal of Qualitative Theory of Differential Equations, vol. 2023, iss. 22, pp. 1-18, 2023.
@article{CarFerNov203c,
title = {Properties of Poincaré half-maps for planar linear systems and some direct applications to periodic orbits of piecewise systems},
author = {Victoriano Carmona and Fernando Fernández Sánchez and Eli García-Medina and Douglas D. Novaes},
url = {https://arxiv.org/abs/2109.12673},
doi = {10.14232/ejqtde.2023.1.22},
year = {2023},
date = {2023-05-24},
urldate = {2023-04-21},
journal = {Electronic Journal of Qualitative Theory of Differential Equations},
volume = {2023},
issue = {22},
pages = {1-18},
abstract = {This paper deals with fundamental properties of Poincaré half-maps defined on a straight line for planar linear systems. Concretely, we focus on the analyticity of the Poincaré half-maps, their series expansions (Taylor and Newton-Puiseux) at the tangency point and at infinity, the relative position between the graph of Poincaré half-maps and the bisector of the fourth quadrant, and the sign of their second derivatives. All these properties are essential to understand the dynamic behavior of planar piecewise linear systems. Accordingly, we also provide some of their most immediate, but non-trivial, consequences regarding periodic orbits.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Victoriano Carmona; Fernando Fernández Sánchez; Douglas D. Novaes
Uniform upper bound for the number of limit cycles of planar piecewise linear differential systems with two zones separated by a straight line Journal Article
Em: Applied Mathematics Letters, vol. 137, pp. 108501, 2023.
@article{CarFerNov2022b,
title = {Uniform upper bound for the number of limit cycles of planar piecewise linear differential systems with two zones separated by a straight line},
author = {Victoriano Carmona and Fernando Fernández Sánchez and Douglas D. Novaes},
url = {https://arxiv.org/abs/2210.12125},
doi = {10.1016/j.aml.2022.108501},
year = {2023},
date = {2023-03-01},
journal = {Applied Mathematics Letters},
volume = {137},
pages = {108501},
abstract = {The existence of a uniform upper bound for the maximum number of limit cycles of planar piecewise linear differential systems with two zones separated by a straight line has been subject of interest of hundreds of papers. After more than 30 years of investigation since Lum-Chua's work, it has remained an open question whether this uniform upper bound exists or not. Here, we give a positive answer for this question by establishing the existence of a natural number $L^*leq 8$ for which any planar piecewise linear differential system with two zones separated by a straight line has no more than $L^*$ limit cycles. The proof is obtained by combining a newly developed integral characterization of Poincaré half-maps for linear differential systems with an extension of Khovanskii's theory for investigating the number of intersection points between smooth curves and a particular kind of orbits of vector fields.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
2022
Douglas D. Novaes; Gabriel A. Rondon
On limit cycles in regularized Filippov systems bifurcating from homoclinic-like connections to regular-tangential singularities Journal Article
Em: Physica D: Nonlinear Phenomena, vol. 441, pp. 133526, 2022.
@article{NovRon2022,
title = {On limit cycles in regularized Filippov systems bifurcating from homoclinic-like connections to regular-tangential singularities},
author = {Douglas D. Novaes and Gabriel A. Rondon},
url = {https://arxiv.org/abs/2005.12986},
doi = {10.1016/j.physd.2022.133526},
year = {2022},
date = {2022-09-07},
journal = {Physica D: Nonlinear Phenomena},
volume = {441},
pages = {133526},
abstract = {In this paper, we are concerned about smoothing of a class of $Sigma$-polycycles of Filippov systems, namely homoclinic-like connections to regular-tangential singularities. Conditions are stablished in order to guarantee the existence of limit cycles bifurcating from such connections.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Douglas D. Novaes
On the Hilbert number for piecewise linear vector fields with algebraic discontinuity set Journal Article
Em: Physica D: Nonlinear Phenomena, vol. 41, pp. 133523, 2022.
@article{Novaes2022,
title = {On the Hilbert number for piecewise linear vector fields with algebraic discontinuity set},
author = {Douglas D. Novaes},
url = {https://arxiv.org/abs/2201.02019},
doi = {10.1016/j.physd.2022.133523},
year = {2022},
date = {2022-09-06},
urldate = {2022-09-06},
journal = {Physica D: Nonlinear Phenomena},
volume = {41},
pages = {133523},
abstract = {The second part of the Hilbert's sixteenth problem consists in determining the upper bound $CH(n)$ for the number of limit cycles that planar polynomial vector fields of degree $n$ can have. For $ngeq2$, it is still unknown whether $CH(n)$ is finite or not. The main achievements obtained so far establish lower bounds for $CH(n)$. Regarding asymptotic behavior, the best result says that $CH(n)$ grows as fast as $n^2log(n)$. Better lower bounds for small values of $n$ are known in the research literature. In the recent paper ``Some open problems in low dimensional dynamical systems'' by A. Gasull, Problem 18 proposes another Hilbert's sixteenth type problem, namely improving the lower bounds for $CL(n)$, $ninN$, which is defined as the maximum number of limit cycles that planar piecewise linear differential systems with two zones separated by a branch of an algebraic curve of degree $n$ can have. So far, $CL(n)geq [n/2],$ $ninN$, is the best known general lower bound. Again, better lower bounds for small values of $n$ are known in the research literature. Here, by using a recently developed second order Melnikov method for nonsmooth systems with nonlinear discontinuity manifold, it is shown that $CL(n)$ grows as fast as $n^2.$ This will be achieved by providing lower bounds for $CL(n)$, which improves every previous estimates for $ngeq 4$.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Paulo R. da Silva; Ingrid S. Meza-Sarmiento; Douglas D. Novaes
Nonlinear sliding of discontinuous vector fields and singular perturbation Journal Article
Em: Differential Equations and Dynamical Systems, vol. 30, pp. 675–693, 2022.
@article{SilMezNov2022,
title = {Nonlinear sliding of discontinuous vector fields and singular perturbation},
author = {Paulo R. da Silva and Ingrid S. Meza-Sarmiento and Douglas D. Novaes},
url = {http://dx.doi.org/10.1007/s12591-018-0439-1
https://arxiv.org/abs/1706.07391},
doi = {10.1007/s12591-018-0439-1},
year = {2022},
date = {2022-07-01},
journal = {Differential Equations and Dynamical Systems},
volume = {30},
pages = {675–693},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Douglas D. Novaes; Leandro A. Silva
On the non-existence of isochronous tangential centers in Filippov vector fields Journal Article
Em: Proceedings of the American Mathematical Society, não 1, pp. 10, 2022.
@article{NovaesLSilva2022,
title = {On the non-existence of isochronous tangential centers in Filippov vector fields},
author = {Douglas D. Novaes and Leandro A. Silva},
url = {https://arxiv.org/abs/2111.09020},
doi = {10.1090/proc/16047},
year = {2022},
date = {2022-07-01},
urldate = {2022-07-01},
journal = {Proceedings of the American Mathematical Society},
number = {1},
pages = {10},
abstract = {The isochronicity problem is a classical problem in the qualitative theory of planar vector fields which consists in characterizing whether a center is isochronous or not, that is, if all the trajectories in a neighborhood of the center have the same period. This problem is usually investigated by means of the so-called period function. In this paper, we are interested in exploring the isochronicity problem for tangential centers of planar Filippov vector fields. By computing the period function for planar Filippov vector fields around tangential centers, we show that such centers are never isochronous. },
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Douglas D. Novaes
An averaging result for periodic solutions of Carathéodory differential equations Journal Article
Em: Proceedings of the American Mathematical Society, vol. 150, não 7, pp. 2945-2954, 2022.
@article{Novaes2022,
title = {An averaging result for periodic solutions of Carathéodory differential equations},
author = {Douglas D. Novaes},
url = {http://arxiv.org/abs/2108.01551},
doi = {10.1090/proc/15810},
year = {2022},
date = {2022-04-14},
journal = {Proceedings of the American Mathematical Society},
volume = {150},
number = {7},
pages = {2945-2954},
abstract = {This paper is concerned with the problem of existence of periodic solutions for perturbative Carathéodory differential equations. The main result provides sufficient conditions on the averaged equation that guarantee the existence of periodic solutions. Additional conditions are also provided to ensure the uniform convergence of a periodic solution to a constant function. The proof of the main theorem is mainly based on an abstract continuation result for operator equations.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
2021
Douglas D. Novaes; Leandro A. Silva
Lyapunov coefficients for monodromic tangential singularities in Filippov vector fields Journal Article
Em: Journal of Differential Equations, vol. 300, não 565, pp. 596, 2021.
@article{NovaesLSilva2021,
title = {Lyapunov coefficients for monodromic tangential singularities in Filippov vector fields},
author = {Douglas D. Novaes and Leandro A. Silva},
url = {http://arxiv.org/abs/2010.00497},
doi = {10.1016/j.jde.2021.08.008},
year = {2021},
date = {2021-11-05},
urldate = {2021-11-05},
journal = {Journal of Differential Equations},
volume = {300},
number = {565},
pages = {596},
abstract = {In planar analytic vector fields, a monodromic singularity can be distinguished between a focus or a center by means of the Lyapunov coefficients, which are given in terms of the power series coefficients of the first-return map around the singularity. In this paper, we are interested in an analogous problem for monodromic tangential singularities of piecewise analytic vector fields Z=(Z+,Z-). More specifically, for positive integers k+ and k-, we consider a (2k+, 2k-)-monodromic tangential singularity, which is defined as an invisible contact of multiplicity 2k+ and 2k- between the discontinuity manifold and, respectively, the vectors fields Z+ and Z- for which a first-return map is well defined around the monodromic tangential singularity. We first prove that such a first-return map is analytic in a neighborhood of the monodromic tangential singularity. This allow us to define the Lyapunov coefficients. Then, as a consequence of a general property for pair of involutions, we obtain that the index of the first non-vanishing Lyapunov coefficient is always even. In addition, a recursive formula for computing all the Lyapunov coefficients is obtained. Such a formula is implemented in a Mathematica algorithm in the appendix. We also provide results regarding limit cycles bifurcating from monodromic tangential singularities. Several examples are analysed.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Douglas D. Novaes
Higher order stroboscopic averaged functions: a general relationship with Melnikov functions Journal Article
Em: Electronic Journal of Qualitative Theory of Differential Equations, vol. 2021, não 77, pp. 1-9, 2021.
@article{NovEJQTDE2021,
title = {Higher order stroboscopic averaged functions: a general relationship with Melnikov functions},
author = {Douglas D. Novaes},
url = {http://www.math.u-szeged.hu/ejqtde/periodica.html?periodica=1¶mtipus_ertek=publication¶m_ertek=9340
http://arxiv.org/abs/2011.03663},
doi = {10.14232/ejqtde.2021.1.77},
year = {2021},
date = {2021-10-09},
journal = {Electronic Journal of Qualitative Theory of Differential Equations},
volume = {2021},
number = {77},
pages = {1-9},
abstract = {In the research literature, one can find distinct notions for higher order averaged functions of regularly perturbed non-autonomous $T$- periodic differential equations of the kind $x'=e F(t,x,e)$. By one hand, the classical (stroboscopic) averaging method provides asymptotic estimates for its solutions in terms of some uniquely defined functions $bg_i$'s, called averaged functions, which are obtained through near-identity stroboscopic transformations and by solving homological equations. On the other hand, a Melnikov procedure is employed to obtain bifurcation functions $f_i$'s which controls in some sense the existence of isolated $T$-periodic solutions of the differential equation above. In the research literature, the bifurcation functions $f_i$'s are sometimes likewise called averaged functions, nevertheless, they also receive the name of Poincar'{e}-Pontryagin-Melnikov functions or just Melnikov functions. While we know that $f_1=T bg_1,$ a general relationship between $bg_i$ and $f_i$ is not known so far for $igeq 2.$ Here, we provide such a general relationship between these two distinct notions of averaged functions, which allows the computation of the stroboscopic averaged functions of any order avoiding the necessity of dealing with near-identity transformations and homological equations. In addition, an Appendix is provided with implemented Mathematica algorithms for computing both higher order averaging functions. },
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Douglas D. Novaes; Gabriel A. Rondon
Smoothing of nonsmooth systems near regular-tangential singularities and boundary limit cycle Journal Article
Em: Nonlinearity, vol. 34, não 6, pp. 4202-4263, 2021.
@article{NovRon2021,
title = {Smoothing of nonsmooth systems near regular-tangential singularities and boundary limit cycle},
author = {Douglas D. Novaes and Gabriel A. Rondon},
url = {https://arxiv.org/abs/2003.09547},
doi = {10.1088/1361-6544/ac04be},
year = {2021},
date = {2021-05-25},
urldate = {2021-05-25},
journal = {Nonlinearity},
volume = {34},
number = {6},
pages = {4202-4263},
abstract = {Understanding how tangential singularities evolve under smoothing processes was one of the first problem concerning regularization of Filippov systems. In this paper, we are interested in Cn-regularizations of Filippov systems around visible regular-tangential singularities of even multiplicity. More specifically, using Fenichel theory and blow-up methods, we aim to understand how the trajectories of the regularized system transits through the region of regularization. We apply our results to investigate Cn-regularizations of boundary limit cycles with even multiplicity contact with the switching manifold.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Victoriano Carmona; Fernando Fernández Sánchez; Douglas D. Novaes
A new simple proof for Lum-Chua's conjecture Journal Article
Em: Nonlinear Analysis: Hybrid Systems, vol. 40, pp. 100992-100999, 2021.
@article{CarFerNov2021,
title = {A new simple proof for Lum-Chua's conjecture},
author = {Victoriano Carmona and Fernando Fernández Sánchez and Douglas D. Novaes},
url = {http://arxiv.org/abs/1911.01372},
doi = {10.1016/j.nahs.2020.100992},
year = {2021},
date = {2021-05-01},
urldate = {2021-05-01},
journal = {Nonlinear Analysis: Hybrid Systems},
volume = {40},
pages = {100992-100999},
abstract = {The already proved Lum-Chua's conjecture says that a continuous planar piecewise linear differential system with two zones separated by a straight line has at most one limit cycle. In this paper, we provide a new proof by using a novel characterization for Poincaré half-maps in planar linear systems.
This proof is very short and straightforward, because this characterization avoids the inherent flaws of the usual methods to study piecewise linear systems (the appearance of large case-by-case analysis due to the unnecessary discrimination between the different spectra of the involved matrices, to deal with transcendental equations forced by the implicit occurrence of flight time, ...).
In addition, the application of the characterization allow us to prove that if a limit cycle exists, then it is hyperbolic and its stability is determined by a simple relationship between the parameters. To the best of our knowledge, the hyperbolicity of the limit cycle and this simple expression for its stability have not been pointed out before.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
This proof is very short and straightforward, because this characterization avoids the inherent flaws of the usual methods to study piecewise linear systems (the appearance of large case-by-case analysis due to the unnecessary discrimination between the different spectra of the involved matrices, to deal with transcendental equations forced by the implicit occurrence of flight time, ...).
In addition, the application of the characterization allow us to prove that if a limit cycle exists, then it is hyperbolic and its stability is determined by a simple relationship between the parameters. To the best of our knowledge, the hyperbolicity of the limit cycle and this simple expression for its stability have not been pointed out before.
Kamila S. Andrade; Oscar A. R. Cespedes; Dayane Cruz; Douglas D. Novaes
Higher order Melnikov analysis of planar piecewise linear vector fields with nonlinear switching curve Journal Article
Em: Journal of Differential Equations, vol. 287, pp. 1-36, 2021.
@article{AndCesCruNov2021,
title = {Higher order Melnikov analysis of planar piecewise linear vector fields with nonlinear switching curve},
author = {Kamila S. Andrade and Oscar A. R. Cespedes and Dayane Cruz and Douglas D. Novaes},
url = {https://arxiv.org/abs/2006.11352},
doi = {10.1016/j.jde.2021.03.039},
year = {2021},
date = {2021-03-29},
urldate = {2021-03-29},
journal = {Journal of Differential Equations},
volume = {287},
pages = {1-36},
abstract = {In this paper, we are interested in providing lower estimations for the maximum number of limit cycles $H(n)$ that planar piecewise linear differential systems with two zones separated by the curve $y=x^n$ can have, where $n$ is a positive integer. For this, we perform a higher order Melnikov analysis for piecewise linear perturbations of the linear center. In particular, we obtain that $H(2)geq 4,$ $H(3)geq 8,$ $H(n)geq7,$ for $ngeq 4$ even, and $H(n)geq9,$ for $ngeq 5$ odd. This improves all the previous results for $ngeq2.$ Our analysis is mainly based on some recent results about Chebyshev systems with positive accuracy and Melnikov Theory, which will be developed at any order for a class of nonsmooth differential systems with nonlinear switching manifold.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Matheus M. Castro; Ricardo M. Martins; Douglas D. Novaes
A note on Vishik's normal form Journal Article
Em: Journal of Differential Equations, vol. 281, não 442-458, 2021.
@article{CasMarNov2021,
title = {A note on Vishik's normal form},
author = {Matheus M. Castro and Ricardo M. Martins and Douglas D. Novaes},
url = {http://arxiv.org/abs/1911.05004},
doi = {10.1016/j.jde.2021.02.011},
year = {2021},
date = {2021-02-11},
journal = {Journal of Differential Equations},
volume = {281},
number = {442-458},
abstract = {The Vishik's Normal Form provides a local smooth conjugation with a linear vector field for smooth vector fields near contacts with a manifold. In the present study, we focus on the analytic case. Our main result ensures that for analytic vector field and manifold, the conjugation with the Vishik's normal form is also analytic. As an application, we investigate the analyticity of Poincaré Half Maps defined locally near contacts between analytic vector field and manifold.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Douglas D. Novaes; Régis Varão
A note on invariant measures for Filippov systems Journal Article
Em: Bulletin des Sciences Mathématiques, vol. 167, pp. 102954, 2021.
@article{NovVar2021,
title = {A note on invariant measures for Filippov systems},
author = {Douglas D. Novaes and Régis Varão},
url = {http://arxiv.org/abs/1706.04212},
doi = {10.1016/j.bulsci.2021.102954},
year = {2021},
date = {2021-01-18},
journal = {Bulletin des Sciences Mathématiques},
volume = {167},
pages = {102954},
abstract = {We are interested in Filippov systems which preserve a probability measure on a compact manifold. We define a measure to be invariant for a Filippov system as the natural analogous definition of invariant measure for flows. Our main result concerns Filippov systems which preserve a probability measure equivalent to the volume measure. As a consequence, the volume preserving Filippov systems are the refractive piecewise volume preserving ones. We conjecture that if a Filippov system admits an invariant probability measure, this measure does not see the trajectories where there is a break of uniqueness. We prove this conjecture for Lipschitz differential inclusions. Then, in light of our previous results, we analyze the existence of invariant measures for many examples of Filippov systems defined on compact manifolds.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Douglas D. Novaes; Francisco B.G. Silva
Higher order analysis on the existence of periodic solutions in continuous differential equations via degree theory Journal Article
Em: SIAM Journal on Mathematical Analysis, vol. 53, não 2, pp. 2476-2490, 2021.
@article{NovGSilva2021,
title = {Higher order analysis on the existence of periodic solutions in continuous differential equations via degree theory},
author = {Douglas D. Novaes and Francisco B.G. Silva},
url = {http://arxiv.org/abs/2006.10799},
year = {2021},
date = {2021-01-05},
urldate = {2021-01-05},
journal = {SIAM Journal on Mathematical Analysis},
volume = {53},
number = {2},
pages = {2476-2490},
abstract = {Recently, the higher order averaging method for studying periodic solutions of both Lipschitz differential equations and discontinuous piecewise smooth differential equations was developed in terms of the Brouwer degree theory. Between the Lipschitz and the discontinuous piecewise smooth differential equations, there is a huge class of differential equations lacking in a higher order analysis on the existence of periodic solutions, namely the class of continuous non-Lipschitz differential equations. In this paper, based on the degree theory for operator equations, we perform a higher order analysis of continuous perturbed differential equations and derive sufficient conditions for the existence and uniform convergence of periodic solutions for such systems. We apply our results to study continuous non-Lipschitz higher order perturbations of a harmonic oscillator.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
2020
Murilo R. Cândido; Douglas D. Novaes; Claudia Valls
Periodic solutions and invariant torus in the Rössler System Journal Article
Em: Nonlinearity, vol. 33, não 9, pp. 4512-4538, 2020.
@article{CanNovVal2020,
title = {Periodic solutions and invariant torus in the Rössler System},
author = {Murilo R. Cândido and Douglas D. Novaes and Claudia Valls},
url = {http://arxiv.org/abs/1903.02398},
doi = {10.1088/1361-6544/ab8bae},
year = {2020},
date = {2020-07-23},
urldate = {2020-07-23},
journal = {Nonlinearity},
volume = {33},
number = {9},
pages = {4512-4538},
abstract = {The Rössler System is characterized by a three-parameter family of quadratic 3D vector fields. There exist two one-parameter families of Rössler Systems exhibiting a zero-Hopf equilibrium. For Rössler Systems near to one of these families, we provide generic conditions ensuring the existence of a torus bifurcation. In this case, the torus surrounds a periodic solution that bifurcates from the zero-Hopf equilibrium. For Rössler Systems near to the other family, we provide generic conditions for the existence of a periodic solution bifurcating from the zero-Hopf equilibrium. This improves currently known results regarding periodic solutions for such a family. In addition, the stability properties of the periodic solutions and invariant torus are analysed.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Douglas D. Novaes; Tere Seara; Marco A. Teixeira; Iris O. Zeli
Study of periodic orbits in periodic perturbations of planar reversible Filippov systems having a two-fold cycle Journal Article
Em: SIAM J. Appl. Dyn. Syst., vol. 19, não 2, pp. 1343-1371, 2020.
@article{NovSeaTeiZel2020,
title = {Study of periodic orbits in periodic perturbations of planar reversible Filippov systems having a two-fold cycle},
author = {Douglas D. Novaes and Tere Seara and Marco A. Teixeira and Iris O. Zeli },
url = {http://arxiv.org/abs/1910.01954},
doi = {10.1137/19M1289959},
year = {2020},
date = {2020-06-01},
urldate = {2020-06-01},
journal = {SIAM J. Appl. Dyn. Syst.},
volume = {19},
number = {2},
pages = {1343-1371},
abstract = {We study the existence of periodic solutions in a class of nonsmooth differential systems obtained from nonautonomous periodic perturbations of reversible piecewise smooth differential systems. It is assumed that the unperturbed system presents a simple two-fold cycle, which is characterized by a closed trajectory connecting a visible two-fold singularity to itself. It is shown that under certain generic conditions the perturbed problem has sliding and crossing periodic solutions. In order to get our results, Melnikov's ideas were applied together with tools from the geometric singular perturbation theory. Finally, a study of a perturbed piecewise Hamiltonian model is performed.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Tiago de Carvalho; Douglas D. Novaes; Luis Fernando Gonçalves
Sliding Shilnikov Connection in Filippov-type Predator-Prey Model Journal Article
Em: Nonlinear Dynamics, vol. 100, pp. 2973-2987, 2020.
@article{deCarNov2020,
title = {Sliding Shilnikov Connection in Filippov-type Predator-Prey Model},
author = {Tiago de Carvalho and Douglas D. Novaes and Luis Fernando Gonçalves},
url = {http://arxiv.org/abs/1809.02060},
doi = {10.1007/s11071-020-05672-w},
year = {2020},
date = {2020-05-13},
journal = {Nonlinear Dynamics},
volume = {100},
pages = {2973-2987},
abstract = {Recently, a piecewise smooth differential system was derived as a model of a 1 predator-2 prey interaction where the predator feeds adaptively on its preferred prey and an alternative prey. In such a model, strong evidence of chaotic behavior was numerically found. Here, we revisit this model and prove the existence of a Shilnikov sliding connection when the parameters are taken in a codimension one submanifold of the parameter space. As a consequence of this connection, we conclude, analytically, that the model behaves chaotically for an open region of the parameter space.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Murilo R. Cândido; Douglas D. Novaes
On the torus bifurcation in averaging theory Journal Article
Em: Journal of Differential Equations, vol. 268, não 8, pp. 4555-4576, 2020.
@article{CanNov2020,
title = {On the torus bifurcation in averaging theory},
author = {Murilo R. Cândido and Douglas D. Novaes},
url = {https://arxiv.org/abs/1810.02992},
doi = {10.1016/j.jde.2019.10.031},
year = {2020},
date = {2020-01-31},
urldate = {2020-01-31},
journal = {Journal of Differential Equations},
volume = {268},
number = {8},
pages = {4555-4576},
abstract = {In this paper, we take advantage of the averaging theory to investigate a torus bifurcation in two-parameter families of 2D nonautonomous differential equations. Our strategy consists in looking for generic conditions on the averaged functions that ensure the existence of a curve in the parameter space characterized by a Neimark-Sacker bifurcation in the corresponding Poincaré map. A Neimark-Sacker bifurcation for planar maps consists in the birth of an invariant closed curve from a fixed point, as the fixed point changes stability. In addition, we apply our results to study a torus bifurcation in a family of 3D vector fields.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
João L. Cardoso; Jaume Llibre; Douglas D. Novaes; Durval J. Tonon
Simultaneous occurrence of sliding and crossing limit cycles in Filippov systems Journal Article
Em: Dynamical Systems: An International Journal, vol. 35, não 3, pp. 490-514, 2020.
@article{CarLliNovTon2020,
title = {Simultaneous occurrence of sliding and crossing limit cycles in Filippov systems},
author = {João L. Cardoso and Jaume Llibre and Douglas D. Novaes and Durval J. Tonon},
url = {https://arxiv.org/abs/1905.06427},
doi = {10.1080/14689367.2020.1722064},
year = {2020},
date = {2020-01-29},
journal = {Dynamical Systems: An International Journal},
volume = {35},
number = {3},
pages = {490-514},
abstract = {In the present study we consider planar piecewise linear vector fields with two zones separated by the straight line x=0. Our goal is to study the existence of simultaneous crossing and sliding limit cycles for such class of vector fields. First, we provide a canonical form for these systems assuming that each linear system has center, a
real one for y<0 and a virtual one for y>0, and such that the real center is a global center. Then working with a first order piecewise linear perturbation we obtain piecewise linear differential systems with three crossing limit cycles. Second, we see that a sliding cycle can be detected after a second order piecewise linear perturbation. Finally, imposing the existence of a sliding limit cycle we prove that only one more crossing limit cycle can appear. In addition, we also characterize the stability of the higher amplitude limit cycle and of the infinity. The main techniques used in our proofs are the Melnikov functions, the Extended Chebyshev systems and the Bendixson
transformation.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
real one for y<0 and a virtual one for y>0, and such that the real center is a global center. Then working with a first order piecewise linear perturbation we obtain piecewise linear differential systems with three crossing limit cycles. Second, we see that a sliding cycle can be detected after a second order piecewise linear perturbation. Finally, imposing the existence of a sliding limit cycle we prove that only one more crossing limit cycle can appear. In addition, we also characterize the stability of the higher amplitude limit cycle and of the infinity. The main techniques used in our proofs are the Melnikov functions, the Extended Chebyshev systems and the Bendixson
transformation.
Jaume Llibre; Douglas D. Novaes; Camila A. B. Rodrigues
Bifurcations from families of periodic solutions in piecewise differential systems Journal Article
Em: Physica D, vol. 404, pp. 132342, 2020.
@article{LliNovRod2020,
title = {Bifurcations from families of periodic solutions in piecewise differential systems},
author = {Jaume Llibre and Douglas D. Novaes and Camila A. B. Rodrigues},
url = {https://arxiv.org/abs/1804.08175},
doi = {10.1016/j.physd.2020.132342},
year = {2020},
date = {2020-01-28},
journal = {Physica D},
volume = {404},
pages = {132342},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Jaume Llibre; Douglas D. Novaes; Iris O. Zeli
Limit cycles of piecewise polynomial perturbations of higher dimensional linear differential systems Journal Article
Em: Revista de Matemátca Iberoamericana, vol. 36, pp. 291-318, 2020.
@article{LliNovZel2019,
title = {Limit cycles of piecewise polynomial perturbations of higher dimensional linear differential systems},
author = {Jaume Llibre and Douglas D. Novaes and Iris O. Zeli},
url = {hyyp://dx.doi.org/10.4171/rmi/1131
https://arxiv.org/abs/1801.01730},
doi = {10.4171/rmi/1131},
year = {2020},
date = {2020-01-01},
urldate = {2020-01-01},
journal = {Revista de Matemátca Iberoamericana},
volume = {36},
pages = {291-318},
abstract = {The averaging theory has been extensively employed for studying periodic solutions of smooth and nonsmooth differential systems. Here, we extend the averaging theory for studying periodic solutions a class of regularly perturbed non--autonomous $n$-dimensional discontinuous piecewise smooth differential system. As a fundamental hypothesis, it is assumed that the unperturbed system has a manifold $CZsubsetR^n$ of periodic solutions satisfying $dim(mathcal{Z})
linear differential systems, $x'=Mx$, when they are perturbed inside
a class of discontinuous piecewise polynomial differential systems
with two zones. More precisely, we study the periodic solutions of
the following differential system
[
x'=Mx+ e F_1^n(x)+e^2F_2^n(x),
]
in $R^{d+2}$ where $e$ is a small parameter, $M$ is a
$(d+2)times(d+2)$ matrix having one pair of pure imaginary
conjugate eigenvalues, $m$ zeros eigenvalues, and $d-m$ non--zero real eigenvalues.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
linear differential systems, $x'=Mx$, when they are perturbed inside
a class of discontinuous piecewise polynomial differential systems
with two zones. More precisely, we study the periodic solutions of
the following differential system
[
x'=Mx+ e F_1^n(x)+e^2F_2^n(x),
]
in $R^{d+2}$ where $e$ is a small parameter, $M$ is a
$(d+2)times(d+2)$ matrix having one pair of pure imaginary
conjugate eigenvalues, $m$ zeros eigenvalues, and $d-m$ non--zero real eigenvalues.
Pedro T. Cardin; Douglas D. Novaes
Asymptotic behavior of periodic solutions in one-parameter families of Liénard equations Journal Article
Em: Journal of Nonlinear Analysis, vol. 190, pp. 111617, 2020, ISBN: 0362-546X.
@article{CardNova2020,
title = {Asymptotic behavior of periodic solutions in one-parameter families of Liénard equations},
author = {Pedro T. Cardin and Douglas D. Novaes},
url = {http://arxiv.org/abs/1705.02362},
doi = {10.1016/j.na.2019.111617},
isbn = {0362-546X},
year = {2020},
date = {2020-01-01},
journal = {Journal of Nonlinear Analysis},
volume = {190},
pages = {111617},
abstract = {In this paper, we consider one--parameter ($la>0$) families of Li'enard differential equations. We are concerned with the study on the asymptotic behavior of periodic solutions for small and large values of $la>0$. To prove our main result we use the relaxation oscillation theory and a topological version of the averaging theory. More specifically, the first one is appropriate for studying the periodic solutions for large values of $lambda$ and the second one for small values of $lambda$. In particular, our hypotheses allow us to establish a link between these two theories.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
2019
Jéfferson L. R. Bastos; Claudio A. Buzzi; Jaume Llibre; Douglas D. Novaes
Melnikov analysis in nonsmooth differential systems with nonlinear switching manifold Journal Article
Em: Journal of Differential Equations, vol. 267, não 5, pp. 3748-3767, 2019.
@article{BBLN2019,
title = {Melnikov analysis in nonsmooth differential systems with nonlinear switching manifold},
author = {Jéfferson L. R. Bastos and Claudio A. Buzzi and Jaume Llibre and Douglas D. Novaes},
url = {http://dx.doi.org/10.1016/j.jde.2019.04.019
https://arxiv.org/abs/1810.02993},
doi = {10.1016/j.jde.2019.04.019},
year = {2019},
date = {2019-09-05},
urldate = {2019-09-05},
journal = {Journal of Differential Equations},
volume = {267},
number = {5},
pages = {3748-3767},
abstract = {We study the family of piecewise linear differential systems in the plane with two pieces separated by a cubic curve. Our main result is that 7 is a lower bound for the Hilbert number of this family. In order to get our main result, we develop the Melnikov functions for a class of nonsmooth differential systems, which generalizes, up to order 2, some previous results in the literature. Whereas the first order Melnikov function for the nonsmooth case remains the same as for the smooth one (i.e. the first order averaged function) the second order Melnikov function for the nonsmooth case is different from the smooth one (i.e. the second order averaged function). We show that, in this case, a new term depending on the jump of discontinuity and on the geometry of the switching manifold is added to the second order averaged function.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Douglas D. Novaes; Marco A. Teixeira
Shilnikov problem in Filippov dynamical systems Journal Article
Em: Chaos, vol. 29, pp. 063110, 2019.
@article{NovTei2019,
title = {Shilnikov problem in Filippov dynamical systems},
author = {Douglas D. Novaes and Marco A. Teixeira},
url = {https://doi.org/10.1063/1.5093067
http://arxiv.org/abs/1504.02425},
doi = {10.1063/1.5093067},
year = {2019},
date = {2019-06-20},
journal = {Chaos},
volume = {29},
pages = {063110},
abstract = {In this paper we introduce the concept of sliding Shilnikov orbits for $3$D Filippov systems. In short, such an orbit is a piecewise smooth closed curve, composed by Filippov trajectories, which slides on the switching surface and connects a Filippov equilibrium to itself, namely a pseudo saddle-focus. A version of the Shilnikov's Theorem is provided for such systems. Particularly, we show that sliding Shilnikov orbits occur in generic one-parameter families of Filippov systems, and that arbitrarily close to a sliding Shilnikov orbit there exist countably infinitely many sliding periodic orbits. Here, no additional Shilnikov-like assumption is needed in order to get this last result. In addition, we show the existence of sliding Shilnikov orbits in discontinuous piecewise linear differential systems. As far as we know, the examples of Fillippov systems provided in this paper are the first exhibiting such a sliding phenomenon.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Leonardo P. C. da Cruz; Douglas D. Novaes; Joan Torregrosa
New lower bound for the Hilbert number in piecewise quadratic differential systems Journal Article
Em: Journal of Differential Equations, vol. 266, não 7, pp. 4170-4203, 2019.
@article{CruNovTor2018,
title = {New lower bound for the Hilbert number in piecewise quadratic differential systems},
author = {Leonardo P. C. da Cruz and Douglas D. Novaes and Joan Torregrosa},
url = {http://dx.doi.org/10.1016/j.jde.2018.09.032
https://arxiv.org/abs/1809.03433},
doi = {10.1016/j.jde.2018.09.032},
year = {2019},
date = {2019-03-15},
urldate = {2019-03-15},
journal = {Journal of Differential Equations},
volume = {266},
number = {7},
pages = {4170-4203},
abstract = {We study the number of limit cycles bifurcating from a piecewise quadratic system. All the differential systems considered are piecewise in two zones separated by a straight line. We prove the existence of 16 crossing limit cycles in this class of systems. If we denote by $H_p(n)$ the extension of the Hilbert number to degree $n$ piecewise polynomial differential systems, then $H_p(2)geq 16.$ As fas as we are concerned, this is the best lower bound for the quadratic class. Moreover, all the limit cycles appear in one nest bifurcating from the period annulus of some isochronous quadratic centers.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
2018
Douglas D. Novaes; Marco A. Teixeira; Iris O. Zeli
The generic unfolding of a codimension-two connection to a two-fold singularity of planar Filippov systems Journal Article
Em: Nonlinearity, vol. 31, pp. 2083–2104, 2018.
@article{NovTeiZel2018,
title = {The generic unfolding of a codimension-two connection to a two-fold singularity of planar Filippov systems},
author = {Douglas D. Novaes and Marco A. Teixeira and Iris O. Zeli},
url = {https://doi.org/10.1088/1361-6544/aaaaf7
https://arxiv.org/abs/1809.03433},
doi = {https://doi.org/10.1088/1361-6544/aaaaf7},
year = {2018},
date = {2018-04-06},
urldate = {2018-04-06},
journal = {Nonlinearity},
volume = {31},
pages = {2083–2104},
abstract = {Generic bifurcation theory was classically well developed for smooth differential systems, establishing results for k-parameter families of planar vector fields. In the present study we focus on a qualitative analysis of 2-parameter families of planar Filippov systems assuming that it presents a codimension-two minimal set for the critical value of the parameter. Such object, named elementary simple two-fold cycle, is characterized by a regular trajectory connecting a visible two-fold singularity to itself, for which the second derivative of the first return map is nonvanishing. We analyzed the codimension-two scenario through the exhibition of its bifurcation diagram.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
2017
Jackson Itikawa; Jaume Llibre; Douglas D. Novaes
A new result on averaging theory for a class of discontinuous planar differential systems with applications Journal Article
Em: Rev. Mat. Iberoam., vol. 33, não 4, pp. 1247-1265, 2017.
@article{ItiLliNov2017,
title = {A new result on averaging theory for a class of discontinuous planar differential systems with applications},
author = {Jackson Itikawa and Jaume Llibre and Douglas D. Novaes},
url = {dx.doi.or/10.4171/rmi/970},
doi = {10.4171/rmi/970},
year = {2017},
date = {2017-11-17},
journal = {Rev. Mat. Iberoam.},
volume = {33},
number = {4},
pages = {1247-1265},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Murilo R. Cândido; Jaume Llibre; Douglas D. Novaes
Persistence of periodic solutions for higher order perturbed differential systems via Lyapunov-Schmidt reduction Journal Article
Em: Nonlinearity, vol. 30, não 9, pp. 3560-3586, 2017.
@article{CanLliNov2016,
title = {Persistence of periodic solutions for higher order perturbed differential systems via Lyapunov-Schmidt reduction},
author = {Murilo R. Cândido and Jaume Llibre and Douglas D. Novaes},
url = {http://doi.org/10.1088/1361-6544/aa7e95
https://arxiv.org/abs/1611.04807},
doi = {10.1088/1361-6544/aa7e95},
year = {2017},
date = {2017-08-14},
urldate = {2017-08-14},
journal = {Nonlinearity},
volume = {30},
number = {9},
pages = {3560-3586},
abstract = {In this work we first provide sufficient conditions to assure the persistence of some zeros of perturbative functions. Then we use this result to compute the bifurcation functions which allow us to study the periodic solutions of T-periodic smooth differential system. It is assumed that the unperturbed differential system has a sub-manifold of periodic solutions. We also study the case when the bifurcation functions have a continuum of zeros. Finally we provide the explicit expressions of the bifurcation functions up to order 5.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Douglas D. Novaes
An equivalente formulation of the averaged functions via Bell polynomials Journal Article
Em: Extended Abstracts Spring 2016: Nonsmooth Dynamics. Trends in Mathematics, vol. 8, pp. 141-145, 2017, ISBN: 978-3-319-55642-0.
@article{NovCRMa2017,
title = {An equivalente formulation of the averaged functions via Bell polynomials},
author = {Douglas D. Novaes},
url = {http://dx.doi.org/10.1007/978-3-319-55642-0_25},
doi = {10.1007/978-3-319-55642-0_25},
isbn = {978-3-319-55642-0},
year = {2017},
date = {2017-05-27},
journal = {Extended Abstracts Spring 2016: Nonsmooth Dynamics. Trends in Mathematics},
volume = {8},
pages = {141-145},
abstract = {We shall use the Bell polynomials to provide an alternative formula for the averaged functions. This new formula can make easier the computational implementation of the averaged functions.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Douglas D. Novaes
Number of limit cycles for some non-generic classes of piecewise linear differential systems Journal Article
Em: Extended Abstracts Spring 2016: Nonsmooth Dynamics. Trends in Mathematics, vol. 8, pp. 135-139, 2017, ISBN: 978-3-319-55642-0.
@article{NovCRMb2017,
title = {Number of limit cycles for some non-generic classes of piecewise linear differential systems},
author = {Douglas D. Novaes},
url = {http://dx.doi.org/10.1007/978-3-319-55642-0_24},
doi = {10.1007/978-3-319-55642-0_24},
isbn = {978-3-319-55642-0},
year = {2017},
date = {2017-05-27},
journal = {Extended Abstracts Spring 2016: Nonsmooth Dynamics. Trends in Mathematics},
volume = {8},
pages = {135-139},
abstract = {Recently, it was provided some upper bounds for the maximum number of limit cycles for some non-generic classes of planar piecewise linear differential systems with two zones separated by a straight line. However many distinct cases were considered. Here we identify the main properties of those classes which allows us to unify the approach and to extend the results. We also study a new class of systems.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Jaume Llibre; Douglas D. Novaes; Camila A. B. Rodrigues
Averaging theory at any order for computing limit cycles of discontinuous piecewise differential systems with many zones Journal Article
Em: Physica D: Nonlinear Phenomena, 2017.
@article{LliNovRod2017,
title = {Averaging theory at any order for computing limit cycles of discontinuous piecewise differential systems with many zones},
author = {Jaume Llibre and Douglas D. Novaes and Camila A. B. Rodrigues},
url = {http://dx.doi.org/10.1016/j.physd.2017.05.003},
doi = {10.1016/j.physd.2017.05.003},
year = {2017},
date = {2017-05-25},
journal = {Physica D: Nonlinear Phenomena},
abstract = {This work is devoted to study the existence of periodic solutions for a class of discontinuous differential systems with many zones. We show that the averaged functions at any order control the existence of crossing limit cycles for systems in this class. We also provide some examples dealing with nonsmooth perturbations of nonlinear centers.
},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Douglas D. Novaes; Joan Torregrosa
On the extended Chebyshev systems with positive accuracy Journal Article
Em: J. Math. Anal. Appl., vol. 488, não 1, pp. 171-186, 2017.
@article{NovTor2017,
title = {On the extended Chebyshev systems with positive accuracy},
author = {Douglas D. Novaes and Joan Torregrosa},
url = {http://dx.doi.org/10.1016/j.jmaa.2016.10.076},
doi = {10.1016/j.jmaa.2016.10.076},
year = {2017},
date = {2017-04-01},
urldate = {2017-04-01},
journal = {J. Math. Anal. Appl.},
volume = {488},
number = {1},
pages = {171-186},
abstract = {A classical necessary condition for an ordered set of n+1 functions F to be an ECT-system in a closed interval is that all the Wronskians do not vanish. With this condition all the elements of Span(F) have at most n zeros taking into account the multiplicity. Here the problem of bounding the number of zeros of Span(F) is considered as well as the effectiveness of the upper bound when some Wronskians vanish. For this case we also study the possible configurations of zeros that can be realized by elements of Span(F). An application to counting the number of isolated periodic orbits for a family of nonsmooth systems is done.
},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Douglas D. Novaes; Gabriel Ponce; Régis Varão
Chaos induced by sliding phenomena in Filippov systems Journal Article
Em: Journal of Dynamics and Differential Equations, pp. 1-15, 2017.
@article{NovPonVar2017,
title = {Chaos induced by sliding phenomena in Filippov systems},
author = {Douglas D. Novaes and Gabriel Ponce and Régis Varão},
url = {http://dx.doi.org/10.1007/s10884-017-9580-8},
doi = {10.1007/s10884-017-9580-8},
year = {2017},
date = {2017-02-16},
journal = {Journal of Dynamics and Differential Equations},
pages = {1-15},
abstract = {In this paper we provide a full topological and ergodic description of the dynamics of Filippov systems nearby a sliding Shilnikov orbit G. More specifically we prove that the first return map, defined nearby G, is topologically conjugate to a Bernoulli shift with infinite topological entropy. In particular, we see that for each natural number m it has infinitely many periodic points with period m.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}