2.
Matheus G. C. Cunha; Douglas D. Novaes; Gabriel Ponce
On the Hausdorff dimension and Cantor set structure of sliding Shilnikov invariant sets Journal Article
Em: Nonlinearity, vol. 37, não 125023, 2024.
@article{CunNovPon2024,
title = {On the Hausdorff dimension and Cantor set structure of sliding Shilnikov invariant sets},
author = {Matheus G. C. Cunha and Douglas D. Novaes and Gabriel Ponce},
url = {https://arxiv.org/abs/2312.10720},
doi = {10.1088/1361-6544/ad8d9c},
year = {2024},
date = {2024-10-31},
urldate = {2024-10-31},
journal = {Nonlinearity},
volume = {37},
number = {125023},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
1.
Douglas D. Novaes; Gabriel Ponce; Régis Varão
Chaos induced by sliding phenomena in Filippov systems Journal Article
Em: Journal of Dynamics and Differential Equations, pp. 1-15, 2017.
@article{NovPonVar2017,
title = {Chaos induced by sliding phenomena in Filippov systems},
author = {Douglas D. Novaes and Gabriel Ponce and Régis Varão},
url = {http://dx.doi.org/10.1007/s10884-017-9580-8},
doi = {10.1007/s10884-017-9580-8},
year = {2017},
date = {2017-02-16},
journal = {Journal of Dynamics and Differential Equations},
pages = {1-15},
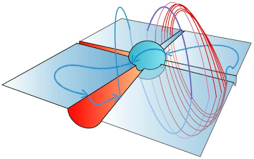
abstract = {In this paper we provide a full topological and ergodic description of the dynamics of Filippov systems nearby a sliding Shilnikov orbit G. More specifically we prove that the first return map, defined nearby G, is topologically conjugate to a Bernoulli shift with infinite topological entropy. In particular, we see that for each natural number m it has infinitely many periodic points with period m.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
In this paper we provide a full topological and ergodic description of the dynamics of Filippov systems nearby a sliding Shilnikov orbit G. More specifically we prove that the first return map, defined nearby G, is topologically conjugate to a Bernoulli shift with infinite topological entropy. In particular, we see that for each natural number m it has infinitely many periodic points with period m.