Definições
Definição:
Sejam V
um
espaço vetorial sobre um corpo K, e
um subconjunto finito de V. O subconjunto U de todos os
elementos
que podem ser escritos como combinação linear dos
elementos de S é um subespaço vetorial denominado Subespaço
Gerado por S.
Definição: S é
denominado Conjunto de
Geradores para U. Dizemos
também que S gera o subespaço U.
Notação: Podemos
escrever U = [] ou U=[S].
Teorema: Seja S um conjunto finito
de elementos de um espaço vetorial V. O conjunto de
todas as combinações lineares dos vetores de S,
denotado por [S], forma um subespaço vetorial de V.
Demonstração: AQUI.
Definição: Um espaço vetorial V é finitamente gerado se existe um subconjunto S V de modo que V = [S].
Exemplos
Exemplo 1: O conjunto gera o subespaço .
De fato, tomando um elemento , temos que , logo podemos escrever:
, com
Dessa forma, mostramos que qualquer
elemento de U pode ser escrito como combinação linear
dos elementos de S, assim, S é um conjunto de geradores
para U.
Geometricamente, o elemento de S é o vetor
e o subespaço U é a reta
,
e de fato, essa reta é gerada pelo vetor
.
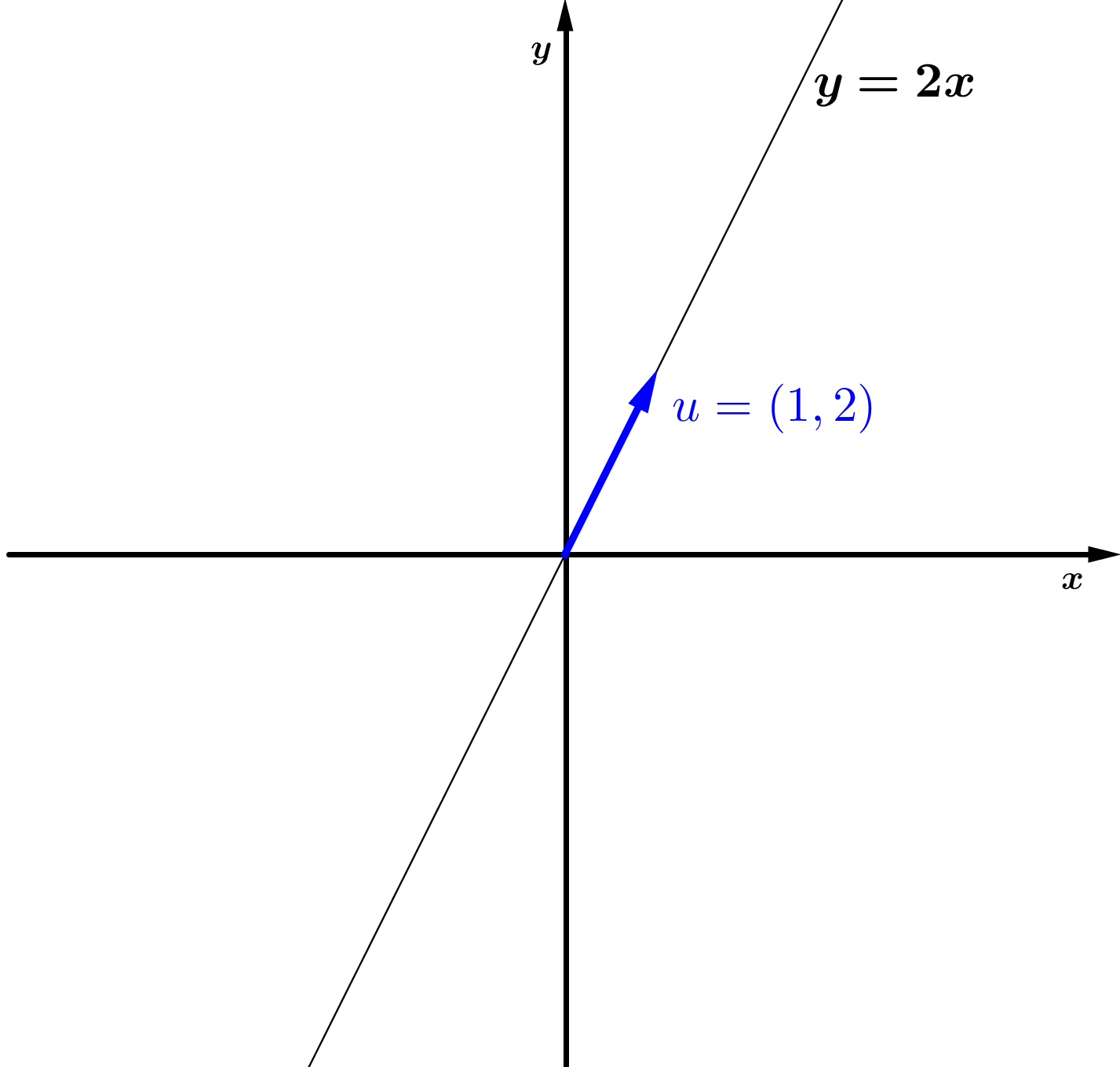
Exemplo 2: O
conjunto
é um conjunto de geradores para o subespaço .
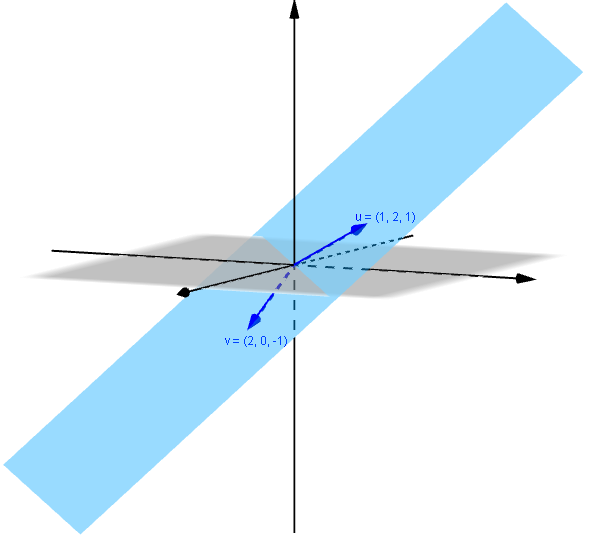
Vamos considerar um elemento qualquer , para que pertença a [S] é preciso que ele possa ser escrito como combinação linear dos elementos de S, ou seja:
Podemos isolar e de qualquer uma das equações, obtendo diferentes resultados. Por exemplo, podemos isolar da primeira equação: e isolar da última equação: , também teremos uma condição sobre , com .
Assim, .
Logo, o conjunto S gera o subespaço dado por:
com e .
Veja estes e mais
exemplos AQUI.