Na sala de aula
Se você é professor de matemática e está trabalhando Geometria Plana ou Análise Combinatória com seus alunos, que tal construir a demonstração ou deduzir a fórmula que determina o número de diagonais de um polígono com eles, ao invés de apenas apresentar uma regrinha pra ser aplicada? Mais ainda, que tal inserir na sua didática o uso de tecnologias para tornar o aprendizado mais divertido e dinâmico?
Vamos definir as propriedades básicas de um polígono e obter a fórmula que determina o número de diagonais destes polígonos de duas maneiras: utilizando Análise Combinatória e utilizando a Indução. Além disso, desenvolvemos um applet no software de Geometria Dinâmica Geogebra que pode te ajudar muito em sala de aula.
Mas antes da demonstração, vamos definir alguns conceitos.

O que é um polígono?
Na Geometria, definimos um polígono como sendo uma figura fechada e com lados. Historicamente, a palavra polígono tem origem do grego “poligonos”, que significa ter muitos lados ou ângulos.
Euclides definia um polígono como uma figura limitada por linhas retas, sendo que essas linhas deveriam ser mais de quatro (curiosamente os triângulos não são chamados por Euclides de polígonos, mas como veremos adiante pela definição formal, eles o são) e essa tal figura seria qualquer região do plano cercada de uma ou mais bordas. Você pode encontrar as definicões de Euclides em [1].
Definição fomal
Dada uma sequência de pontos de um plano \((A_1,\;A_2,\; …,\; A_n)\) com \(n\geq 3\), todos distintos, onde três pontos consecutivos não são colineares, considerando-se consecutivos \(A_{n-1}\), \(A_n,\) e \(A_1\), assim como \(A_n\), \(A_1\) e \(A_2\), chama-se polígono à reunião dos segmentos \(\overline{A_1A_2}\), \(\overline{A_2A_3}\), …, \(\overline{A_{n-1}A_n}\), \(\overline{A_n,A_1}\).
Por exemplo, são polígonos:

Mas não são polígonos:
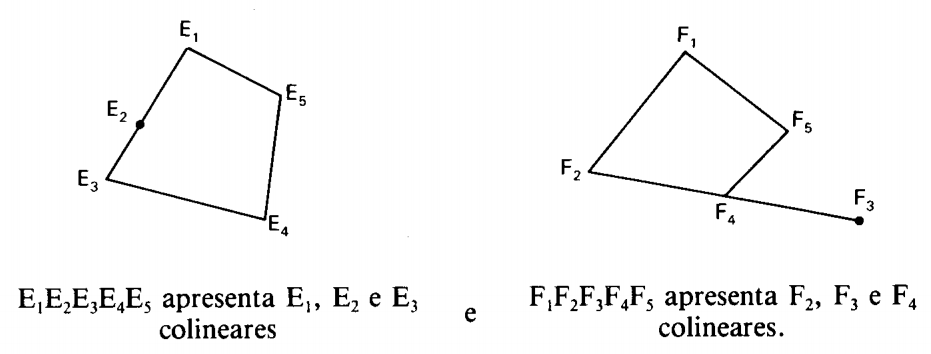
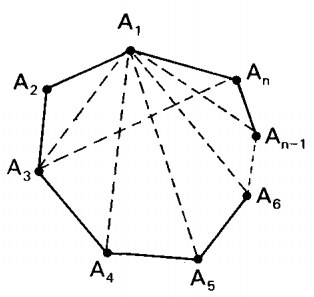
- Os pontos \(A_1,\;A_2,\; …,\; A_{n-1},\; A_n\) são os vértices do polígono.
- Os segmentos \(\overline{A_1A_2},\;\overline{A_2A_3},\; …,\;\overline{A_{n-1}A_n},\;\overline{A_nA_1}\) são os lados do polígono.
- Os ângulos \(\hat{A_1}=A_n\hat{A_1}A_2\), \(\hat{A_2}=A_1\hat{A_2}A_3\), …, \(\hat{A_n}=A_{n-1}\hat{A_n}A_1\) são os ângulos do polígono.
Polígono simples: Um polígono é simples se, e somente se, a interseção de quaisquer dois lados não consecutivos é vazia (eles não se encontram nunca). Caso contrário é dito complexo. Note que os polígonos anteriores \(A_1A_2A_3A_4A_5\) e \(B_1B_2B_3B_4B_5\) são simples, enquanto \(C_1C_2C_3C_4C_5\) e \(D_1D_2D_3D_4D_5\) não são.
Polígono convexo: Um polígono simples é convexo se, e somente se, a reta determinada por dois vértices consecutivos quaisquer deixa todos os demais \((n-2)\) vértices num mesmo semiplano dos dois que ela determina (ficam todos de um mesmo lado da reta). Por exemplo:

Diagonais de um polígono
Diagonal: Definimos uma diagonal de um polígono como o segmento cujas extremidades são dois lados não consecutivos do polígono. Note que as diagonais estāo presentes em qualquer tipo de polígono.
Agora sim, temos todas as ferramentas básicas necessárias para enunciar e deduzir a seguinte propriedade:
O número de diagonais \(d\) de um polígono de \(n\) lados \((n \geq 3)\) é dado por:
$$d=\frac{n(n-3)}{2}$$
Dedução - propriedade combinatória
Comentários: Nesta dedução, iremos obter a fórmula para o número de diagonais de um polígono. A importância deste método, além da sua interdisciplinaridade entre a Geometria e a Indução é que este método incentiva o desenvolvimento do raciocínio matemático do aluno, que consegue notar padrões e construir conjecturas.
Você pode começar mostrando aos alunos uma tabela, assim como Duarte usa em [2], com alguns polígonos simples cujos números de diagonais é fácil de determinar, e daí ir fazendo questionamentos sobre padrões e sobre uma fórmula geral.
Dedução: Seja \(A_1A_2…A_{n-1}A_n\) um polígono de \(n\) lados. Escolhendo um dos vértices do polígono, sem perda de generalidade, teremos \((n-3)\) diagonais, visto que com três vértices (o que escolhemos e seu dois vizinhos) não poderemos formar diagonais.
Como escolhendo um vértice como extremidade temos \((n-3)\) diagonais, então como o polígono possui \(n\) vértices, teremos no total \(n(n-3)\) diagonais.
Mas ao fazermos esta conta, cada uma das diagonais é contada duas vezes, pois possui duas extremidades, uma em cada vértice. (por exemplo, se considerassemos a conta anterior, estariamos contando \(\overline{A_1A_3}\) e \(\overline{A_3A_1}\) como duas diagonais diferentes, quando na verdade são a mesma).
Portanto, o número de diagonais de um polígono é: \(d=\frac{n(n-3)}{2}\).
Demonstração - Fórmula equivalente
Preparação: Antes de começarmos, precisamos apresentar o seguinte raciocínio:
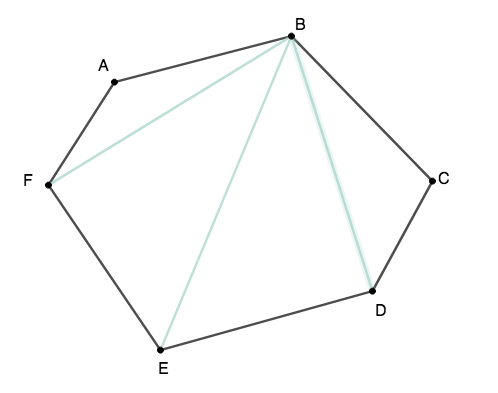
Usando o hexágono \(ABCDEF\) como exemplo, vamos analisar cada um de seus vértices.
Temos que do vértice \(A\) saem três diagonais: \(\overline{AC}\), \(\overline{AD}\) e \(\overline{AE}\). (note que o vértice \(A\) e seus dois vértices vizinhos não podem formar diagonais neste caso). Então, em \(A\) temos \((6-3)\) diagonais.

Considerando o vértice \(B\), também temos três diagonais partindo dele, que são \(\overline{BD}\), \(\overline{BE}\) e \(\overline{BF}\). Novamente, \(B\) e seus vizinhos não formam diagonais e temos em \((6-3)\) diagonais em \(B\).
Em \(C\) teremos apenas duas diagonais, \(\overline{CE}\) e \(\overline{CF}\) pois se a diagonal \(\overline{CA}\) é a mesma que \(\overline{AC}\), que já contamos anteriormente. Com isso, temos 4 vértices a menos para formar diagonal com \(C\), e não somente 3 como anteriormente. Temos portanto \((6-4)\) partindo deste vértice
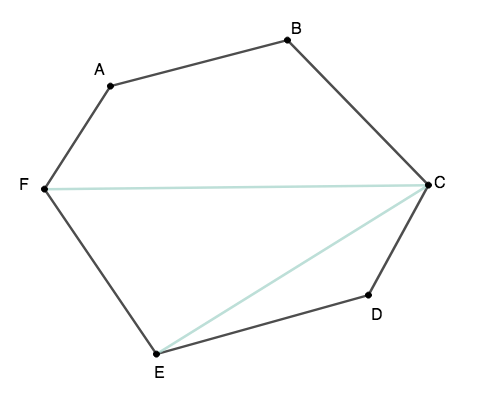
Com o mesmo raciocínio, no vértice \(D\) teremos apenas uma diagonal \(\overline{DF}\), pois todas as outras possibilidades foram contadas.
Neste caso, teremos 5 vértices a menos para formar diagonais e teremos portanto um total de \((6-5)\) diagonais partindo do vértice \(D\).
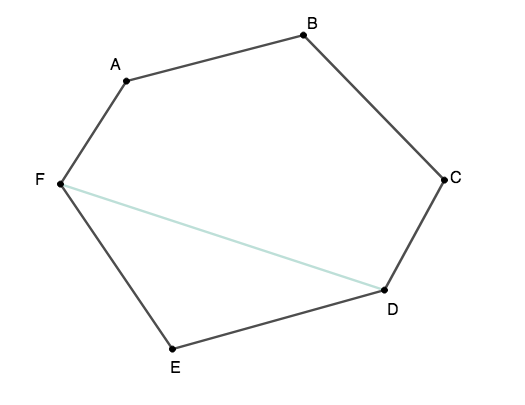
Por fim, não teremos mais nenhuma diagonal em nossa conta, pois se considerássemos mais alguma estaríamos contando-a duas vezes. Então, o total de diagonais do polígono será dado por: \(3+3+2+1=9\). Se utilizarmos o mesmo processo para um octógono por exemplo, teríamos \((8-3)+(8-3)+(8-4)+(8-5)+(8-6)+(8-7)=5+5+4+3+2+1=20\) diagonais, o que pode ser verificado com nossa fórmula anterior.
Mas mesmo que fizéssemos inúmeros exemplos, não estaríamos demonstrando a validade desta propriedade para os infinitos polígonos existentes e, para fazer isso, utilizaremos a indução finita.
Como vimos em nosso raciocínio, o número de diagonais de um polígono de \(n\) lados é dado por
$$d=(n-3)+(n-3)+(n-4)+(n-5)+…+3+2+1$$
o que vamos fazer é provar a validade da fórmula fechada.
Demonstração direta: Vamos primeiramente mostrar que \(d=(n-3)+(n-3)+(n-4)+(n-5)+…+3+2+1=\frac{n(n-3)}{2}\).
Desenvolvendo nossa expressão:
$$d=(n-3)+(n-3)+(n-4)+(n-5)+…+[n-(n-3)]+[n-(n-2)]+[n-(n-1)]$$
Reorganizando a soma:
$$d=n+n+n+…+n-3-3-4-5-…-(n-2)-(n-1)$$
Agora notando que temos um total de \((n-2)\) \(n\)‘s e \(-3=-1-2\) obtemos:
$$d=n\cdot (n-2)-[1+2+3+4+…+(n-1)]$$
Mas note que \(1+2+3+4+…+(n-1)=\frac{n(n+1)}{2}-n\) (esse é um dos primeiros exercícios que fazemos com indução) e substituindo em \(d\) segue que:
$$d=n\cdot (n-2)-\frac{n(n+1)}{2}+n=\frac{n^2-3n}{2}=\frac{n(n-3)}{2}$$
Demonstração por indução:
Caso base: Se \(n=3\), temos um triângulo, que não possui diagonais: \(d=3-3=0\) ok
Hipótese de indução: Suponha que a propriedade valha para \(n=k\), isto é, o número de diagonais de um polígono de \(k\) lados seja dado por:
$$d=(k-3)+(k-3)+(k-4)+(k-5)+…+3+2+1$$
Vamos verificar que ela também vale para um polígono de \(k+1\) lados, isto é,
$$d=(k+1-3)+(k+1-3)+(k+1-4)+(k+1-5)+…+3+2+1$$
$$=(k-2)+(k-2)+(k-3)+(k-4)+…+3+2+1$$
Temos pela hipótese de inducão que:
$$(k-3)+(k-3)+(k-4)+(k-5)+…+3+2+1=\frac{k(k-3)}{2}$$
e então:
$$\frac{k(k-3)}{2}-(k-3)=(k-3)+(k-4)+(k-5)+…+3+2+1$$
substituindo esta expressão em \(d_{k+1}\):
$$d=(k-2)+(k-2)+\frac{k(k-3)}{2}-(k-3)$$
e colocando tudo no mesmo denominador teremos:
$$d=\frac{k^2-k-2}{2}=\frac{(k+1)(k-2)}{2}=\frac{(k+1)(k+1-3)}{2}$$
como queríamos.
Desenvolvemos um applet que professores e alunos podem manipular em sala de aula e em casa, que exibe as diagonais de um polígono e a relação do número de diagonais com o número de lados. Você pode encontrar esse e outros materiais do Geogebra em nosso perfil ou usar aqui mesmo!
No Geogebra
Fontes:
[1] Wikisource. Page:The Elements of Euclid for the Use of Schools and Colleges. Disponível em: <https://en.wikisource.org/wiki/Page:The_Elements_of_Euclid_for_the_Use_of_Schools_and_Colleges_-_1872.djvu/27>. Acesso em 4 jun 2020.
[2] DUARTE, E. A. Princípio da Indução Finita em conteúdos do Ensino Médio. PROFMAT. 2015. Disponível em: <https://repositorio.ufc.br/handle/riufc/47714>. Acesso em: 30 out 2025.
[3] DOLCE, O. POMPEO, J. N. Fundamentos de Matemática Elementar Vol. 9: Geometria Plana. 7ed.