Rita, dá licença

Na minha última postagem, apresentei situações de uma multiplicação de dois números com dois algarismos para exemplificar o quê eu vejo como sendo os conhecimentos específicos que professores e professoras que ensinam Matemática precisam ter para exercerem sua profissão.

Por conta de algumas atividades atuais, resolvi dar um passo para trás e, antes de seguir para um conteúdo mais “avançado”, resolvi escrever sobre adição.

É bem provável que muitas crianças já tenham contato com adições e subtrações desde muito cedo, em casa com a família ou com amigos. Uma formalização dessas operações é apresentada nos Anos Iniciais do Ensino Fundamental. Idealmente, essa formalização é cercada de conceitos que explorem e elucidem sobre o sistema decimal de numeração… na prática, muitas crianças são expostas, repetidamente, ao algoritmo (também conhecido como “arme e efetue”) e só são avaliadas por ter decorado ou não o tal algoritmo da adição e da subtração.

Minha pergunta seria: Precisamos mesmo que as crianças decorem um algoritmo para adição? Não seria melhor compreender o sistema decimal de numeração e as propriedades das operações, saber estimar resultados e usar calculadoras?

Vamos pensar um pouco mais sobre essa coisa de algoritmo da adição e o conhecimento específico que professores que ensinam Matemática, precisam ter. Resolvendo a conta 45 + 17 pelo algoritmo mais tradicionalmente usado, teríamos:

• cinco mais sete é doze, escreve o 2 e vai um;
• quatro mais um mais um é seis escreve o seis.

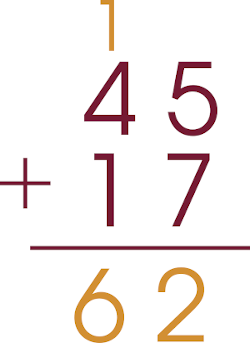
É curto para escrever, é curto para falar, é rápido… ótimo, por isso é um algoritmo largamente difundido.

Mas professores que ensinam matemática (em qualquer fase de escolarização) precisam saber e ser capazes de justificar o “vai um”. Pense um pouco… o que é esse “vai um”?

Você deve saber, que o “vai um” é uma dezena que foi formada ao adicionarmos 5 unidades e 7 unidades e o estudante também precisa saber disso, mesmo que depois ele/ela automatizem esse procedimento.

É preciso lembrar (e isso faz parte das atribuições de professores) que estudantes já devem ter feito adições usando material manipulativo como tampinhas e diversos outros objetos concretos! Também já devem ter tido contato com o material dourado (cubinhos para unidade, barrinha com 10 cubinhos para dezena, placa com dez barrinhas para a centema e etc). Apenas pedir que decorem “quando a soma passar de 9 vai um” é ignorar tudo que os estudantes já sabiam e poderiam usar de alicerce para tornar o algoritmo tradicional menos abstrato.

Minha sugestão é, antes de apresentar o algoritmo tradicional da adição, peça para que a sua turma registre no papel uma adição que você escolher da forma como os estudantes preferirem. A partir disso, escolha algumas para serem discutidas e apresentadas na lousa. Aqui vão dois exemplos muito úteis para essa transição - que podem não aparecer nos registros dos seus estudnates, mas você pode usar mesmo assim.

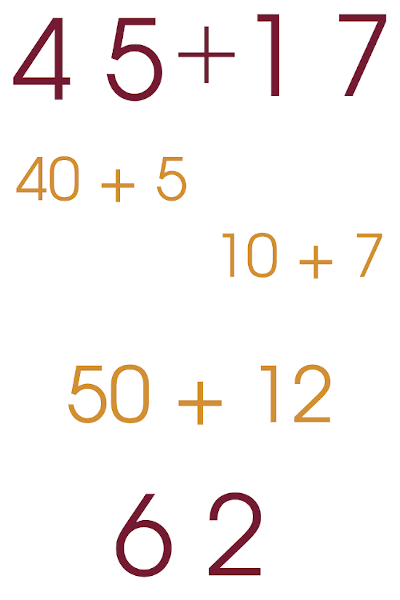
Você entende o que a estudante fez para chegar ao resultado? Professores que ensinam Matemática precisam ser capazes de aceitar, comentar, e (na minha opinião) parabenizar uma resolução como essa! Notem os destaques na imagem a seguir, que sugerem o que a estudante fez para chegar ao resultado.

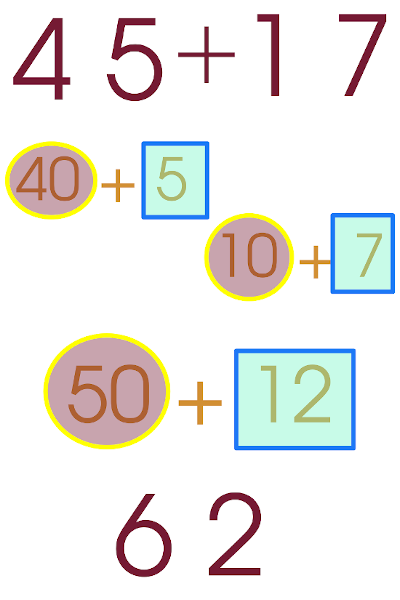
Essa resolução, além de sugerir que a estudante é bastante fluente em decompor números corretamente, permite supor esse método pode virar um processo mental, sem a necessidade de representação no papel, dessa estudante e ela consiga resolver muitas adições “de cabeça” em um futuro muito próximo (bastaria ela ter a certeza de que esse método é válido e útil, receber incentivo e ter acesso a novos exemplos que aprimorem seu raciocínio no sentido de expandir a técnica – tudo isso sendo parte do trabalho de professor).

Para quem ainda quer “armar uma conta”, que tal usar este algoritmo intermediário?

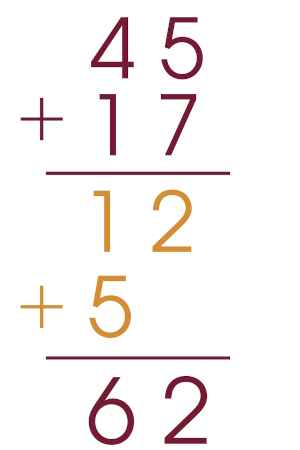
Nesse caso, armamos a conta assim como no algoritmo tradicional, mas o resultado da primeira adição (5 + 7 = 12) de fato está registrado no papel! Não é bem mais intuitivo? Note que bastou o 1 das dezenas (do 12) ficar alinhado com a ordem das dezenas das parcelas sendo adicionadas. A segunda etapa é adicionar 4 dezenas (do 47) e 1 dezena (do 15), obtendo 5 dezenas, que também ficam representadas no papel – na coluna adequada, já que são 5 dezenas. Por fim, precisamos adicionar esses resultados parciais para obter o resultado final da conta original.

Gosto muito desses exemplos de métodos “alternativos” para a adição e acredito que crianças serão beneficiadas se forem expostas a eles e tiverem a oportunidade de considerar e discutir como e por quê eles funcionam! Os benefícios (no caso, aprendizagens) dessas considerações vão muito além do que se poderia obter com uma lista de “arme e efetue”, você não acha?

Como de costume, fique à vontade para discordar e para perguntar, afinal, aqui é dá licença…

Uma afirmação, já bem aceita, é que ninguém ensina o que não sabe. Em Matemática, uma pergunta natural que segue essa afirmação é: mas que Matemática professoras e professores precisam saber para ensinar?

Este é um tópico de pesquisa na área de Educação Matemática e tem tido diversos avanços muito interessantes em termos de compreender:

• que conhecimento (matemático) é esse;
• como professores desenvolvem tais conhecimentos.

Este texto é focado em futuros professores e professores atuantes, não vou falar de avanços em pesquisa científica, mas deixarei algumas sugestões de onde buscar referências, combinado? Quero apresentar algumas considerações minhas sobre exemplos que eu gosto muito e que oferecem bons indícios de quais são os conhecimentos específicos que professores e professoras de Matemática precisam ter e, principalmente, como eles são diferentes de conhecimento Matemático de matemáticos profissionais.

Em especial, vou focar em conteúdos do Ensino Fundamental. De qualquer forma, quero comentar que este texto, mesmo sendo apenas minha seleção de alguns exemplos, pode ser de interesse para professores e para formadores de professores.
Último comentário antes do primeiro exemplo: já notei que vou precisar de mais de um texto.
A seguir, apresento apenas o primeiro (acompanhe o blog para não perder o segundo exemplo).

Exemplo 1: multiplicação

Retirado de: BALL, Deborah Loewenberg; HILL, Heather C; BASS, Hyman. Knowing mathematics for teaching: Who knows mathematics well enough to teach third grade, and how can we decide? American Educator, Washington, EUA, v. 29, n. 3, 2005. – texto publicado por uma associação de professores dos EUA.
Adoro esse subtítulo que os autores usaram, numa tradução livre: “quem sabe matemática suficiente para ensinar crianças da terceira série?”.

A Ball e a Hill são pesquisadoras da área de Educação Matemática e o Bass é matemático. Eles trabalharam juntos em muitos artigos e projetos sobre o tema “conhecimento do professor de matemática” (busque por esses nomes no Google Acadêmico e você terá leitura por um bom tempo).
Eis um exemplo que eles usaram, traduzido e com meus comentários:

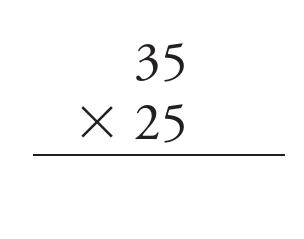
Quase todo mundo que terminou o Ensino Básico ainda deve se lembrar de como resolver a multiplicação acima. Todos os professores de matemática devem saber executar o algoritmo que resulta no resultado correto ilustrado na próxima figura.

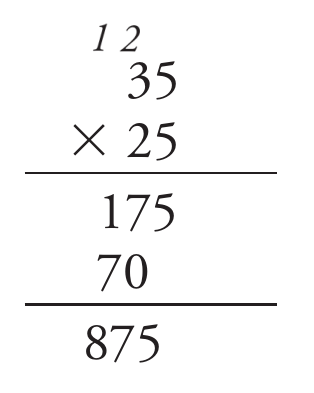
Mas dar uma aula sobre multiplicação não é resolver uma multiplicação enquanto os alunos assistem. Professores “precisam explicar, ouvir e examinar resoluções de estudantes. Eles precisam ser capazes de escolher bons exemplos e modelos. Essas ações exigem mais perspicácia e compreensão de Matemática.” (p. 17). Por exemplo, para notar que a resolução a seguir está errada. E ir além, considerar que a resolução está errada apenas por um deslize no posicionamento dos termos ou há algo mais?

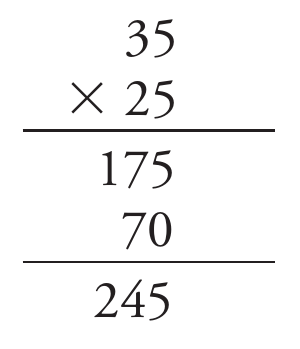
Identificar o procedimento errado é necessário, mas também é preciso notar que a resposta final deveria ter chamado a atenção de estudante, não seria 245 um valor pequeno demais já que 25×4 já formam 100?
E agora? Qual foi o erro?

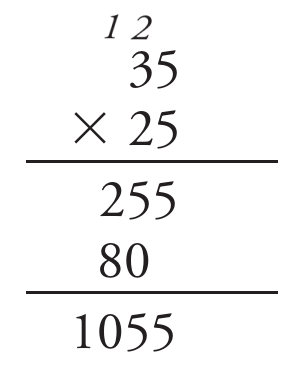
Um pouco mais difícil de imaginar, certo?
Os alunos podem explicar suas soluções e esse é um tipo de atividade bastante rica, mas com 30, 40 alunos na sala, não é viável fazer tal dinâmica o tempo todo. Tudo isso, lembrando que os alunos também pedem explicações e justificativas.

Na primeira resolução errada, como você explicaria que está fazendo 35×20 e não só 35×2 como aparece na conta?
Além da possibilidade de falar sobre (e escrever) as ordens e falar sobre a decomposição dos números, os professores precisam saber usar diferentes representações. Como esta, usando o modelo de área:

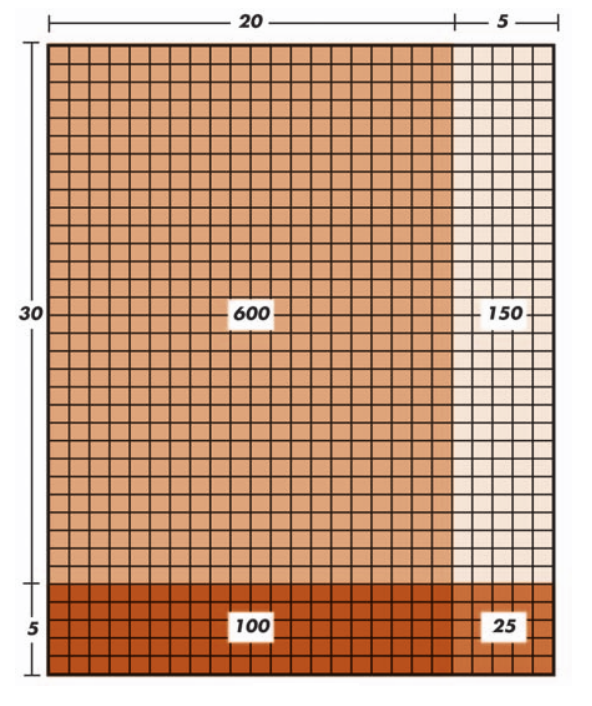
Qual é a área de um retângulo de lados 25 e 35? (Preciso escolher unidades?). Só que, para poder usá-la de forma produtiva, seus alunos precisam estar cientes do que representa comprimento e o que representa a área (Quanto esses conceitos já estão cristalizados para que possam ser usados como fundamento para um outro conteúdo?). Por quê, ou melhor, o quê desse retângulo representa a multiplicação inicial? E como essa representação ajuda na explicação das etapas do algoritmo?

Se um aluno, depois ter visto essa representação, resolver a multiplicação assim:

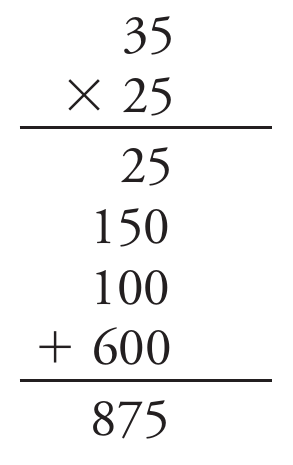
Tudo bem? É preciso fazer alguma sugestão, algum alerta?

E se outro aluno resolver assim:

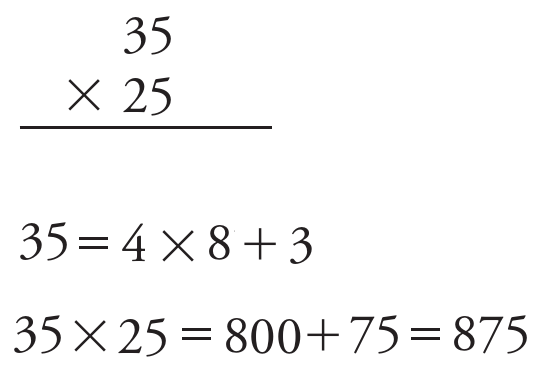
Com essa resolução não algorítmica (e correta), aproveito para comentar sobre a importância de escolher exemplos e determinar a sequência na qual se pretende apresentar atividades.
Será que 35 x 25 é um bom exemplo para justificar o algoritmo tradicional? Não seria melhor ter usado 12 x 43, onde não tem nenhum “vai um”? A representação no modelo retangular vai ficar razoável com essas novas multiplicações?

Engenheiros/as, arquitetos/as e economistas precisam ser capazes de discutir essas questões para executar bem os seus trabalhos? Do meu ponto de vista, de jeito nenhum! Na escola, as explicações e justificativas que fazem sentido para os alunos e que são ancoradas em conhecimentos anteriores permitem o desenvolvimento de novos conhecimentos, e isso não significa que o aluno é capaz de elaborar uma aula de multiplicação de números com dois algarismos. Isso é atribuição de professores de Matemática, que têm que criar situações na sala de aula onde 30 estudantes diferentes consigam “dar sentido” ao conhecimento em foco no momento.
Os autores do texto seguem argumentando sobre a necessidade de “medir” esse tipo de conhecimento. O texto é de 2005, e depois de muito desenvolvimento nessa vertente de “criar testes para medir”, a primeira autora já se afastou desse foco para valorizar a observação de professores em atuação como forma de desenvolver tais conhecimentos. Enfim, não é o meu objetivo aqui discutir como medir se um professor tem esse conhecimento ou não, e avaliação é uma área enorme e com muitos objetivos diferentes.

A mensagem final que quero deixar, e o texto da Ball, Hill e Bass também destaca, é “unless we, as educators, are willing to claim that there is professional knowledge that matters for the quality of instruction and can back that claim with evidence, we will continue to be no more than one voice among many competing to assert what teachers should know.”(p. 46). Traduzindo: a menos que nós, educadores, estivermos dispostos a reivindicar que existe um conhecimento profissional que faz a diferença em termos de ser capaz de dar boas aulas e pudermos dar suporte a essa reivindicação com evidências, nós vamos continuar sendo apenas mais uma voz entre várias competindo para afirmar o que professores devem saber.

Nos comentários do post vamos falar dessa multiplicação, ok? Fique à vontade para discordar e para perguntar, afinal, aqui é dá licença…