Elipses no multiverso?
Desde a antiguidade, na Grécia, dois problemas centrais preocupavam à humanidade: a queda de corpos na Terra e o movimento dos astros. Partindo dessas questões e do conhecimento limitado acerca do universo, diversas teorias surgiram com objetivo de descrever o movimento dos astros.
Se você ja está ansiosa(o) para saber qual a aplicação matemática aqui, já adiantamos que a queridíssima Elipse, da Geometria Analítica, é quem configura a órbita de todos os planetas do Sistema Solar. Mas não foi tão simples determinar isso. Na verdade foram necessários séculos de estudos.
E que tal você conhecer um pouquinho sobre toda essa história?

Sistema Geocêntrico
A primeira teoria foi a do Geocentrismo, uma ideia que perdurou por toda a Antiguidade e Idade Média, e dentre os filósofos que defendiam esta teoria, o mais conhecido é Aristóteles.
Este sistema, também é conhecido como sistema ptolomaico em homenagem a Cláudio Ptolomeu (Claudius Ptolemaeus 150 D.E.C), pois foi este que construiu o modelo geocêntrico mais completo.
Ptolomeu propôs que o movimento dos planetas ocorria através de uma combinação de círculos: o planeta se move ao longo de um pequeno círculo chamado epiciclo, cujo centro se move em um círculo maior chamado deferente. A Terra fica numa posição um pouco afastada do centro do deferente (portanto o deferente é um círculo excêntrico em relação à Terra). Para dar conta do movimento não uniforme dos planetas, Ptolomeu introduziu ainda o equante, que é um ponto ao lado do centro do deferente oposto à posição da Terra, em relação ao qual o centro do epiciclo se move a uma taxa uniforme.


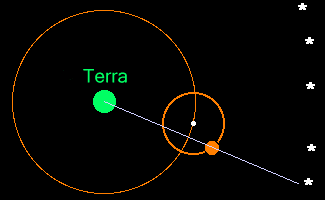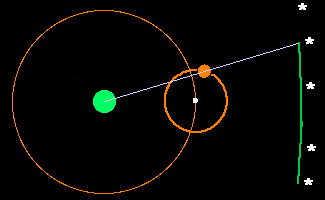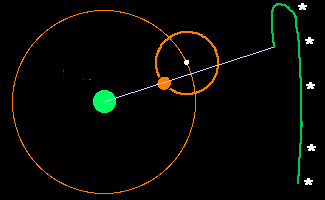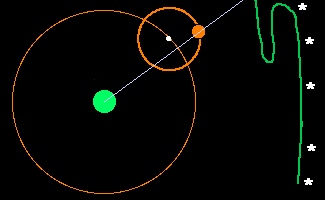
O objetivo de Ptolomeu era produzir um modelo que permitisse prever a posição dos planetas de forma correta. Nessa questão, ele obteve algum sucesso e por isso, esse modelo continuou sendo usado sem mudança significativa por 1300 anos.
Usando o conceito dos epiciclos, Ptolomeu conseguiu então explicar as órbitas que não eram circulares quando vistas da Terra.
A ideia geocêntrica predominou até que o astrônomo e matemático polonês Nicolau Copérnico (1473-1543), resgatou uma hipótese igualmente antiga, a hipótese heliocêntrica, criada pelo astrônomo grego Aristarco de Samos (310-230 a.C.).
Sistema Heliocêntrico
O fim da ocupação árabe na península ibérica marca o início da renascença, e com esse movimento, inicia-se a tradução de textos árabes e gregos, que trazem à Europa conhecimentos de Astronomia, Matemática, Biologia e Medicina. Nicolau Copérnico, (1473-1543), astrônomo polonês com grande inclinação para a matemática, em seus estudos na Itália leu sobre a hipótese heliocêntrica proposta por por Aristarco ( 300 a.C.), antes não aceita, e viu mais sentido em se ter o Sol no centro do Universo do que a Terra. Copérnico então registrou suas idéias no livro – De Revolutionibus – publicado no ano de sua morte.
Em sua teoria, Copérnico:
- introduziu a ideia de que a Terra é apenas um dos seis planetas (então conhecidos) girando em torno do Sol
- colocou os planetas em ordem de distância ao Sol: Mercúrio, Vênus, Terra, Marte, Júpiter, Saturno (Urano, Netuno e o planeta anão Plutão).
- determinou as distâncias dos planetas ao Sol, em termos da distância Terra-Sol.
- deduziu que quanto mais perto do Sol está o planeta, maior é sua velocidade orbital. Dessa forma, o movimento retrógrado dos planetas foi facilmente explicado sem necessidade de epiciclos.

Porém, Copérnico manteve a ideia de que as órbitas dos planetas eram circulares, e embora o movimento dos planetas ficasse simples de entender no seu sistema, as posições previstas para os planetas não eram melhores do que as posições previstas no sistema de Ptolomeu.
A Teoria Heliocêntrica de copérnico conseguiu dar explicações simples sobre fenômenos como o movimento retrógrado dos planetas. Contudo, Copérnico não conseguiu prever as posições dos planetas de uma forma precisa e tampouco conseguiu provar que a Terra também estava em movimento.

Além desse sistema, Copérnico deduziu a escala relativa de distâncias no sistema solar. A distância Sol-Terra (rT ) é hoje a unidade astronômica (U.A.).
Então, para contribuir e construir todo o entendimento sobre as órbitas dos astros que temos hoje, surgem três nomes com contribuições enormes neste ramo da física: Tycho, Kepler e Galileu.
Tycho Brahe
O dinamarquês Tycho Brahe (1546-1601), foi o último grande astrônomo observacional antes da invenção do telescópio. Usando instrumentos de fabricação própria, ele fez muitas observações acerca das posições dos planetas e estrelas, e com uma precisão em muitos casos melhor do que 1 minuto de arco (1/30 do diâmetro aparente do Sol). Em seu livro Astronomiae instauratae mechanica, de 1598, ele descreve como desenvolveu e utilizou quatro tipos diferentes de esferas armilares (instrumento que consta de um modelo reduzido do cosmo), melhores do que as de Hiparcos e as de Ptolomeu, descritas no Syntaxis de Ptolomeu. Tycho podia medir diretamente as coordenadas eclípticas ou equatoriais dos objetos celestes, com as esferas, enquanto seus outros instrumentos mediam coordenadas horizontais (altura e azimute). Sua maior esfera armilar tinha 2,6 metros de diâmetro, e ele descreveu que a maior fonte de erro era a flexão e deslocamento dos círculos (armillae, em latim), devido ao seu próprio peso.


Com o apoio do rei da Dinamarca, Frederic II, Tycho pode construir seu próprio observatório, na pequena ilha báltica de Hven (entre Dinamarca e Suécia).
Tycho Brahe não acreditava na hipótese heliocêntrica de Copérnico, mas foram suas observações dos planetas que levaram às leis de Kepler do movimento planetário.
Em 1600 (um ano antes de sua morte), Tycho contratou para ajudá-lo na análise dos dados sobre os planetas, colhidos durante 20 anos, um jovem e hábil matemático alemão chamado Johannes Kepler.
Johannes Kepler
Johannes Kepler sob influência dos escritos de Copérnico, era um defensor do heliocentrismo que em 1594 conseguiu um posto de professor de matemática e astronomia em uma escola secundária em Graz, na Áustria, mas poucos anos depois, por pressões da Igreja Católica (Kepler era protestante), foi exilado, e foi então para Praga trabalhar com Tycho Brahe.
Quando Tycho morreu, Kepler ocupou seu posto e ficou com seus dados, se dedicando aos estudos destes pelos 20 anos seguintes.
Marte era o planeta que mais possuía dados, com isso Kepler conseguiu determinar as diferentes posições da Terra após cada período sideral de Marte, e assim conseguiu traçar a órbita da Terra, percebendo que essa órbita era muito bem ajustada por um círculo excêntrico, isto é, com o Sol um pouco afastado do centro.
Embora as órbitas dos planetas sejam elipses (1ª lei de Kepler), as excêntricidades são tão pequenas que elas se parecem com círculos.

Kepler conseguiu também determinar a órbita de Marte, mas não conseguiu ajustá-la com um círculo. Então continuou insistindo nessa tentativa por vários anos, e encontrou uma órbita circular que concordava com as observações com um erro de 8 minutos de arco. Mas sabendo que as observações de Tycho não poderiam ter um erro desse tamanho (apesar disso significar um erro de apenas 1/4 do tamanho do Sol), Kepler descartou essa possibilidade.
Passou então a tentar representar a órbita de Marte com uma forma oval, e descobriu que uma elipse ajustava bem aos dados. (O indiano Aryabhata I (476-550), escreveu em seu tratado de astronomia e matemática, Aryabhatiya, que as órbitas dos planetas em torno do Sol deveriam ser elipses). A posição do Sol coincidia com um dos focos da elipse e assim foi explicada também a trajetória quase circular da Terra, com o Sol afastado do centro.
Embora as órbitas dos planetas sejam elipses, as excentricidades são tão pequenas que elas se parecem com círculos.
Em decorrência de todos os estudos de Kepler, ele pode postular três leis universais, conhecidas como leis de Kepler.
Leis de Kepler
1ª. Lei das órbitas elípticas (Astronomia Nova, 1609): Todos os planetas se movem em órbitas elípticas, com o Sol em um dos seus focos.

Onde:
\(a\) – semieixo maior
\(e = \frac{c}{a} \) – excentricidade da elipse (quando muito pequena, a elipse se parece com uma esfera)
\(m\) – representa o planeta
\(F\) e \(F’ \) – focos da elipse
\(Rp\) – distância do periélio (ponto mais próximo do sol)
\(Ra\) – distância do afélio (ponto mais afastado do sol)
2ª. Lei da áreas (1609): A reta que une um planeta ao Sol varre áreas iguais no plano da órbita do planeta em intervalos de tempo iguais. (isto é, a taxa de variação \(dA/dt\) da área com o tempo é constante).
Com isso, temos que a velocidade dos planetas em torno do Sol é variada, sendo maior quando estão no periélio (mais perto do Sol) do que quando estão no afélio (longe do Sol); Tente entender o motivo disto observando a imagem.

3ª. Lei harmônica (Harmonices Mundi, 1618): O quadrado do período de qualquer planeta é diretamente proporcional ao cubo de sua distância média ao Sol (semieixo maior da orbita).
Esta lei estabelece que planetas com órbitas maiores se movem mais lentamente em torno do Sol e, portanto, isso implica que a força entre o Sol e o planeta decresce com a distância ao Sol.
Galileu Galilei
Uma grande contribuição ao Modelo Heliocêntrico foi dada pelo italiano Galileu Galilei (1564 – 1642), que foi o pai da moderna física experimental e da astronomia telescópica. Seus experimentos em mecânica estabeleceram parte dos conceitos de inércia, e de que a aceleração de corpos em queda livre não depende de seu peso, que foram mais tarde incorporados às leis do movimento de Newton.
Galileu começou suas observações telescópicas em 1609, usando um telescópio construído por ele mesmo. Porem não é de Galileu o crédito da invenção do telescópio, pois lentes e óculos já eram conhecidos desde cerca de 1350, e Galileu tinha ouvido falar do telescópio construído pelo holandês Hans Lippershey (1570-1619) em 1608. Galileu soube desse instrumento em 1609, e, sem ter visto o telescópio de Lippershey, construiu o seu próprio, com aumento de 3 vezes, em 1609. Em seguida ele construiu outros instrumentos, e o melhor tinha aumento de 30 vezes.
Galileu usou o telescópio para observar o céu e com isso:
- descobriu que a Via Láctea era constituída por uma infinidade de estrelas.
- descobriu que Júpiter tinha quatro satélites, ou luas, orbitando em torno dele, com períodos entre 2 e 17 dias. Esses satélites são chamados “galileanos”, e são: Io, Europa, Ganimedes e Calisto. Desde então, mais 57 satélites foram descobertos em Júpiter. Essa descoberta de Galileu foi particularmente importante porque mostrou que podia haver centros de movimento que por sua vez também estavam em movimento; portanto o fato da Lua girar em torno da Terra não implicava que a Terra estivesse parada.
- descobriu que Vênus passa por um ciclo de fases, assim como a Lua.



Essa descoberta foi importante, pois no sistema ptolomaico Vênus está sempre mais próximo da Terra do que o Sol, e como Vênus está sempre próximo do Sol, ele nunca poderia ter toda sua face iluminada voltada para nós (fase cheia) e, portanto, deveria sempre aparecer como nova ou no máximo crescente. Mas ao ver que Vênus muitas vezes aparece em fase quase totalmente cheia, Galileu concluiu que ele viaja ao redor do Sol, passando às vezes pela frente dele e outras vezes por trás dele, e não revolve em torno da Terra.
- descobriu a superfície em relevo da Lua, e as manchas do Sol. Ao ver que a Lua tem cavidades e elevações como a Terra, e que o Sol também não tem a superfície lisa, mas apresenta marcas, provou que os corpos celestes não são esferas perfeitas, mas têm irregularidades, assim como a Terra.
As descobertas de Galileu serviram de evidências ao sistema heliocêntrico e, por disso, ele foi chamado a depor ante a Inquisição Romana, sob acusação de heresia, e obrigado a se retratar. Galileu foi perdoado em 31 de outubro de 1992.
P.S A razão (principal) da proibição da Igreja ao heliocentrismo era que no Salmo 104:5 do Antigo Testamento da Bíblia, está escrito: Deus colocou a Terra em suas fundações, para que nunca se mova.
Fontes
HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos de física. 9. ed. Rio de Janeiro, RJ: LTC, c2012 vol 2.
Movimento dos planetas. Disponível em: <https://brazilastronomy.wordpress.com/movimento-dos-planetas/>. Acesso em 26 fev. 2020.