Assim como as parábolas, as elipses têm uma propriedade que as tornam especiais, e muito aplicáveis no mundo real. Se trata de propriedade refletora da elipse, e dessa propriedade refletora, a qual iremos provar e estudar em breve, decorre o seguinte:
Se uma fonte de luz ou som é colocada ao mesmo tempo no foco de uma superfície com seções transversais elípticas, então toda a luz ou som é refletido da superfície para o outro foco
As galerias de Sussurros
As galerias de sussurros são geralmente circulares, hemisféricas, elípticas ou elipsoidais, e muitas vezes são construídas sob uma cúpula ou uma abóbada. (elas também podem ser montadas usando dois ramos parabólicos).
A propriedade interessante destas galerias, é que se uma pessoa posicionada em um ponto específico sussurrar algo, outra pessoa, posicionada também em um ponto específico, pode ouvi-la, mesmo que o resto da sala não consiga. Geralmente, estes pontos específicos são os focos da forma que configura a sala.
No caso das salas com a forma de uma elipse ou elipsóide (estas são as mais interessantes), como por exemplo na Catedral de São Paulo (Saint Paul), que foi a primeira galeria de sussurros, fundada em 1710, em Londres, e o Grand Central Terminal, em Manhattan, New York, os sons são refletidos através dos focos.
A base da explicação desse fenômeno é dada pela propriedade refletora da Elipse, que será nosso objeto de estudo de hoje.

Mas antes de conhecer toda a teoria, que tal presenciar de perto esse fenômeno, curtindo um dueto educativo direto do Grand Central Terminal?
Para que a afirmação: “Quando uma onda sonora se origina em um foco de uma galeria de sussurros, a onda sonora será refletida na cúpula elíptica e voltada para o outro foco”, fique mais clara, observe a figura abaixo.
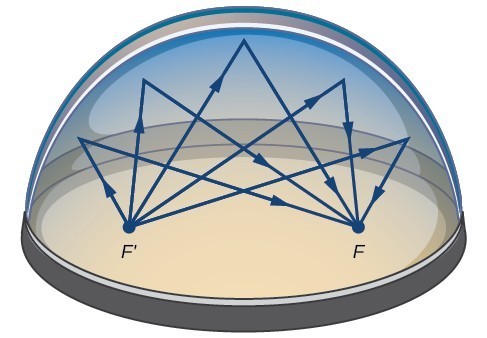
Mas agora, pra entender e provar essa propriedade, vamos conhecer as elipses e algumas de suas características. O leitor curioso sobre o assunto, pode consultar nossas referências.
Conhecendo a elipse e suas propriedades
- O lugar geométrico \( E \) dos pontos \( X \) tais que \( d(X, F_1) + d(X, F_2) = 2a \) chama-se elipse.
- Cada um dos pontos \( F_1 \) e \( F_2 \) é chamado de foco da elipse, o segmento \( F_1 F_2 \) é chamado de segmento focal, seu ponto médio de centro da elipse e o tamanho \( 2c \) de distância focal.
- A reta \( F_1 F_2 \) chama-se reta focal, e qualquer segmento cujas extremidades (distintas) pertencem a \( E \) chama-se corda da elipse.

Obtendo a equação geral da Elipse
Para deduzir a equação da elipse, escolhendo um sistema ortogonal de coordenadas com \( F_1 = (-c, 0) \) e \( F_2 = (c, 0) \) (focos sobre o eixo das abscissas), sabemos que \( X = (x,y) \) pertence a elipse se, e somente se \( d(X, F_1) + d(X, F_2) = 2a \), ou seja, se e somente se, \( d(X, F_1) = 2a \ – \ d(X, F_2) \) e temos:
$$ \sqrt{(x+c)^2 + y^2} = 2a \ – \ \sqrt{(x-c)^2 + y^2} $$
para remover as raízes, elevamos ambos os membros ao quadrado e, simplificamos, o que resulta em:
$$ a\sqrt{(x-c)^2 + y^2} = a^2 – cx $$
Elevando novamente ao quadrado, obtemos
$$ a^2[(x-c)^2 + y^2] = a^4 – 2a^2cx + c^2x^2 $$
que é equivalente a
$$ (a^2 – c^2)x^2 + a^2y^2 = a^2(a^2 – c^2) $$
Para simplificarmos ainda mais esta equação, seja \( b = \sqrt{a^2 – c^2}\), então, \( a^2 = b^2 + c^2 \) e podemos escrever a equação como \( b^2 x^2 + a^2 y^2 = a^2 b^2 \). Por fim, dividindo ambos os membros por \( a^2 b^2 \), obtemos a equação geral da elipse:
$$ \frac{x^2} {a^2} + \frac{y^2} {b^2} = 1 $$
E um ponto \( X = (x,y) \) pertence à elipse se, e somente se, satisfaz a equação anterior.
Obs.: Note que nos passos anteriores, elevamos a expressão duas vezes ao quadrado. Então, para garantir que podemos fazer isso com segurança, sem que existam pontos que não pertencem à elipse mas satisfazem sua equação, vamos provar o seguinte:

Proposição: Um ponto \( X = (x,y) \) é um ponto da elipse de equação reduzida \( x^2 / a^2 + y^2 / b^2 = 1 \) se, e somente se, as distâncias de \( X \) aos focos \( F_1 \) e \( F_2 \) são:
$$ d(X, F_1) = a + \frac{cx} {a} \quad \text{e} \quad d(X, F_2) = a \ – \frac{cx} {a} $$
Veja que é suficiente mostrar a ida, pois a volta está clara, uma vez que das expressões de \( d(X, F_1) \) e \( d(X, F_2) \), resulta \( d(X, F_1) + d(X, F_2) = 2a \) e portanto, \( X \) pertence à elipse (pela definição).
Supondo agora que \( X = (x,y) \) e \( x^2 / a^2 + y^2 / b^2 = 1 \), temos:
$$ y^2 = b^2 \ – \ b^2 x^2 / a^2 $$
e portanto:
$$ \begin{align*} d^2(X,F_1)& = (x+c)^2+y^2 \\ & = x^2+2cx+c^2+b^2-\frac{b^2x^2}{a^2} \\ & = \frac{(a^2-b^2)x^2}{a^2}+2cx+c^2+b^2 \\ & = \frac{c^2x^2}{a^2} +2cx+a^2=( \frac{cx}{a}+a)^2 \end{align*} $$
veja que usamos a relação \( a^2 = b^2 + c^2 \). Do mesmo modo, obtemos que \( d^2(X,F_2)=(\frac{cx}{a}-a)^2 \) e, tirando as raízes, segue que:
$$ \begin{align*} & d(X, F_1) = \left| \frac{cx} {a} + a \right| \\[3mm] & d(X, F_2) = \left| \frac{cx} {a} \ – \ a \right| \end{align*} $$
Da hipótese, temos \( x^2 / a^2 + y^2 / b^2 = 1 \) e, resulta que \( x^2 / a^2 \le 1 \Rightarrow |x| \le a \).
Multiplicando a equação por \( c / a > 0\), obtemos \( c |x|/a \le c \le a \) e pelas propriedades do módulo \( -a \le cx/a \le a \) e, portanto \( cx/a + a \ge 0\) e \( cx/a \ – a \le 0 \).
Agora podemos eliminar os módulos das expressões de \( d(X, F_1) \) e \( d(X, F_2) \) obtendo: \( d(X,F_1) = a + cx/a \) e \( d(X, F_2) = a \ – cx/a \). Portanto, \( d(X,F_1) + (X,F_2) = 2a \)
Com isso, temos que todo ponto que satisfaz a equação reduzida da elipse, pertence à elipse.
A propriedade refletora da Elipse
Lema 1: Sejam \( \vec{u} = \vec{AB} \) e \( \vec{v} = \vec{AC} \) vetores não nulos de normas \(b\) e \(c\) respectivamente. Então o vetor \( \vec{w} = c \vec{u} + b \vec{v} \) é paralelo à bissetriz de \( B \hat{A} C \).
Para mostrar \( \vec{w} = c \vec{u} + b \vec{v} \) é paralelo à bissetriz de \( B \hat{A} C \), devemos mostrar que o o ângulo entre \( \vec{u} \) e \( \vec{w} \) é igual ao ângulo entre \( \vec{v} \) e \( \vec{w} \).
Usando o produto escalar entre vetores, sabemos que se \( \theta = ang \left( \vec{i}, \vec{j} \right) \) então \( \cos\theta=\frac{\vec{i} \cdot \vec{j}}{ || \vec{i} || \ || \vec{j} || } \) . Assim,
$$ \cos\theta_1 = \frac{\vec{u} \cdot (c\vec{u} + b\vec{v})}{b \lVert \vec{w} \rVert} = \frac{1}{\lVert \vec{w} \rVert} \left( \frac{c}{b} \lVert \vec{u} \rVert^2 + \vec{u} \cdot \vec{v} \right) = \frac{1}{\lVert \vec{w} \rVert} \left( \frac{c}{b} b^2 + \vec{u} \cdot \vec{v} \right) = \frac{1}{\lVert \vec{w} \rVert} \left( cb + \vec{u} \cdot \vec{v} \right) $$
$$ \cos\theta_2 = \frac{\vec{v} \cdot (c\vec{u} + b\vec{v})}{c \lVert \vec{w} \rVert} = \frac{1}{\lVert \vec{w} \rVert} \left( \frac{b}{c} \lVert \vec{v} \rVert^2 + \vec{u} \cdot \vec{v} \right) = \frac{1}{\lVert \vec{w} \rVert} \left( \frac{b}{c} \cdot c^2 + \vec{u} \cdot \vec{v} \right) = \frac{1}{\lVert \vec{w} \rVert} \left( cb + \vec{u} \cdot \vec{v} \right) $$
Como o angulo entre dois vetores é sempre definido como o menor deles \( (0^{\circ} \le \theta \le 180^{\circ}) \), temos que \( \cos \theta_1 = \cos \theta_2 \Rightarrow \theta_1 = \theta_2 \) e neste caso, \( \vec{w} \) é paralelo à bissetriz de \( B \hat{A} C \).
Lema 2: O vetor normal à elipse \( \textbf{E}:x^2/a^2+y^2/b^2=1 \) em \( T = (h,k) \) é dado por \( \vec{n} = (b^2 h, a^2 k) \).
Este lema não exige grande abstração e não é de difícil demonstração, mas por exigir algumas definições prévias sobre retas tangentes e normais à elipse,que não é nosso objetivo aqui, vamos omitir sua demonstração.
O leitor curioso pode consultar o livro de referência para tal.
Proposição: Seja \( T = (h,k) \) um ponto da elipse \( \textbf{E}:x^2/a^2+y^2/b^2=1 \). A reta \(s\), normal a \( E \) no ponto \( T \) , contém a bissetriz do ângulo \( E_1 \hat{T} F_2 \).

Sejam \( F_1 = (-c,0) \) e \( F_2 = (c,0) \) os focos da elipse. Usando o lema anterior, é suficiente mostrar que o vetor \( \vec{u}=\lVert \vec{TF_2} \rVert \ \vec{TF_1} + \lVert \vec{TF_1} \rVert \ \vec{TF_2} \) é não nulo e paralelo ao vetor normal à elipse em \(T\), \( \vec{n} = (b^2 h, a^2 k) \). (neste caso, a reta \( s \), normal à elipse em \( T \), e que têm como direção o vetor \( \vec{n} \), será a bissetriz de \( F_1 \hat{T} F_2 \))
Usando a proposição anterior, temos que \( \lVert \vec{TF_1} \rVert = a + ch/a \) e \( \lVert \vec{TF_2} \rVert = a \ – \ ch/a \).
Então, as coordenadas de \( \vec{u} \) são:
\begin{align*} u_1 & = (a \ – \frac{ch}{a})(-c-h) + (a + \frac{ch}{a})(c-h)\\[2mm] & = -ac-ah + \frac{c^2h}{a} + \frac{ch^2}{a} + ac-ah + \frac{c^2h}{a}-\frac{ch^2}{a} \\[2mm] & = -2ah + \frac{2c^2h}{a} = \frac{-2h(a^2 – c^2)}{a} = \frac{-2b^2h} {a} \\[7mm] u_2 & = (a \ – \frac{ch}{a})(-k) + (a + \frac{ch}{a})(-k) \\[2mm] & = (a \ -\frac{ch}{a} + a + \frac{ch}{a})(-k) = -2ak \end{align*}
Logo,
$$ \vec{u} = \left( -\frac{2b^2h}{a},-2ak \right) = \frac{-2}{a} \left( b^2h,a^2k \right) = -\frac{2}{a}\vec{n} $$
e assim, provamos que \( \vec{u} \) é não nulo e é paralelo a \( \vec{n} \),
Neste caso, reta \(s\), normal a \(E\) no ponto \(T\), contém a bissetriz do ângulo \( F_1 \hat{T} F_2 \).
Elipsóide: uma extensão das elipses
Um elipsóide consiste basicamente da revolução de uma elipse em torno de sua reta focal.
Então, você deve imaginar que a propriedade refletora da elipse, se estende também para o elipsoide, e isso explica o fenômeno ocorrido nas salas silenciosas.
Quer ver essa propriedade de perto? Preparamos um applet no Geogebra pra você!
Outras aplicações
Elipses e o dentista
Os dentistas também aproveitam das propriedades da elipse em suas luminárias com espelhos elípticos, que possuem a propriedade de concentrar os raios luminosos em um ponto, que é ajustado pelo dentista para iluminar o dente que está sendo tratado. com isso, os dentistas conseguem duas vantagens:
A primeira é concentrar o máximo de luz onde se está trabalhando, e a segunda é evitar que os raios luminosos ofusquem o paciente, o que aumentaria o desconforto causado pelo tratamento dentário.
Pedras nos rins
O fato que uma fonte de luz ou som colocada no foco de uma superfície com seções transversais elípticas, refletido da superfície para o outro foco, também tem aplicações na litotripsia, um tratamento para pedras nos rins.
Em resumo, um refletor com seção elíptica é posicionado de maneira que a pedra nos rins esteja em um dos focos e então, ondas sonoras de alta intensidade geradas no outro foco são refletidas na pedra e a destroem sem danificar o tecido ao redor.

Fontes
BOULOS, P. & CAMARGO, I. Geometria Analítica – Um Tratamento Vetorial. 3a. ed. São Paulo: Prentice Hall, 2005
954 Conic Sections: Ellipses: Applications: Lithotripsy & Whispering Galleries + Elliptical Artwork. Jul. 2017. Disponível em: <https://onedrive.live.com/?authkey=%21ALWtFcD0IwCFlVM&cid=88862EF47BCAF6CD&id=88862EF47BCAF6CD%21113892&parId=88862EF47BCAF6CD%21113887&o=OneUp>. Acesso em: mar. 2020.
VALLADARES, R. J. C. Elipse, sorrisos e sussurros. RPM 36. Disponível em <http://www.rpm.org.br/cdrpm/36/5.htm>. Acesso em: mar. 2020.