O que aconteceu na 5ª SEMAP:
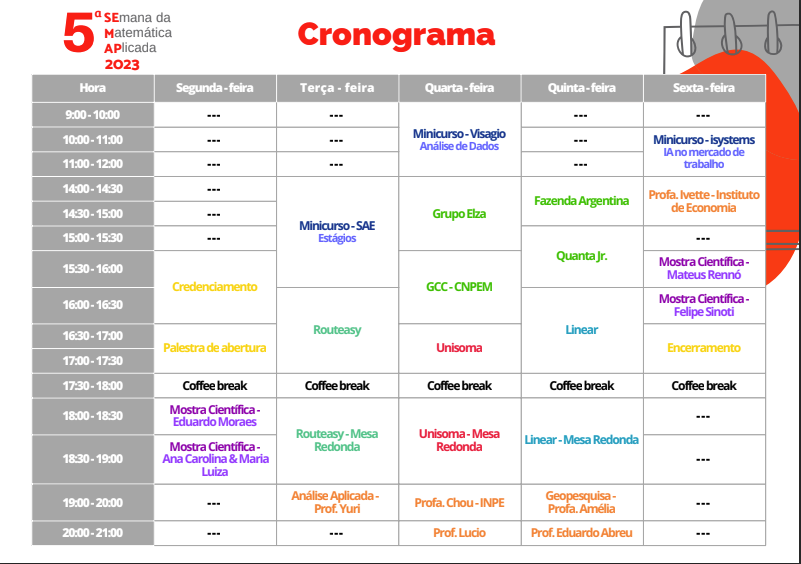
Confira o Cronograma, Mostra Científica, Organizadores e muito mais da nossa edição de 2023
Palestras Acadêmicas
Professores do IMECC
Tivemos palestras de professores tanto sobre Grupos de Pesquisa quanto de áreas de atuação de matemátios aplicados
Minicursos
Slide 3 Sub Title
IAsystem: como usam IA para predição de estoques e vendas, a VISAGIO :como usar python para desenvolver modelos de aprendizado de máquina e o SAE: como construir um currículo e se portar em uma entrevista de emprego
Institutos de Pesquisa
Palestras
Pela primeira vez tivemos um pesquisador no INPE apresentando na SEMAP. A pesquisadora Chou Sin Chan revelou mais uma grande área que os matemáticos podem desbravar
Organização

Lucas Moura

Isabella Letícia Rossi Grutzmann

Milena Lumi Hangai

Gabriela Aparecida Nogueira Honorato

Matheus Brito

Matheus Schyindt

Maria Eduarda da Silva Faria

Mateus Dogan

Isabella Jeske Rosa

Beatriz Julião Reis

Gabriel Reis Barros Santana

Viviane Moura
Mostra Científica
- All Posts
- 2023
Aluna: Laryssa Abdala
O presente trabalho tem o objetivo de simular um fluxo sanguíneo através de uma das cavidades do coração, por exemplo, um ventrículo. O modelo matemático bidimensional da câmara cardíaca, aqui proposto, resultou em uma modificação da equação de Navier-Stokes, a qual é aproximada usando o método dos elementos finitos. A abordagem numérica é apresentada, assim como os resultados das simulações realizadas.
Aluna: Joyce Climaco
É comum pensarmos que os grandes trabalhos atuais da física se dão nas escalas quânticas ou astronômicas, i.e., extremamente pequenas ou grandes. Porém, existe outro limite para o qual os comportamentos físicos ainda apresentam muitos mistérios: a quatidade. Conseguimos modelar com certa facilidade sistemas dinâmicos individuais, porém ainda carecemos de técnicas para modelar o comportamento de muitos destes sistemas interagindo entre si. É nesse contexto que surge o estudo de redes complexas, que buca descrever o comportamento de diversos objetos com uma dinâmica específica ligados com alguma determinada configuração. O acoplamento desses sistemas pode fazer com que eles passem a seguir um mesmo tipo de trajetória no espaço de fase, ou no caso de osciladores, que eles passem a oscilar juntos numa mesma fase e frequência. Esse último fenômeno é chamado de sincronização, e é extensamente estudado atualmente devido à quantidade de suas aplicações que vão desde redes elétricas até a batida das células de um coração ou as sinapses coordenadas num conjunto de neurônios. O modelo de Kuramoto foi o primeiro a propor uma formulação matemática para lidar com conjunto de osciladores que sincronizam suas fases, se aproveitando-se bastante de analogias com física estatística. Variações desse modelo são então constantemente estudadas por serem capazes de descrever diferentes aspectos do fenômeno de sincronização, e assim gerar novas descobertas e aplicações.
Aluno: Vinícius Wasques
Dentre os diversos problemas modelados em matemática aplicada, abordaremos dois assuntos: problemas de valores iniciais e o método de mínimos quadrados. Na prática, as informações que obtemos de fenômenos da natureza são incertos/imprecisos. Visando modelar essa incerteza, lidaremos com esses dois tópicos sob o ponto de vista fuzzy, levando em conta possíveis relações intrínsecas de dependência entre as variáveis envolvidas, as quais serão modeladas pelo que chamamos de interatividade fuzzy.
Aluno: Ivan Nascimento
O objetivo desta exposição é o de introduzir, através de uma aplicação prática, o problema de decompor uma dada matriz como a soma de uma matriz esparsa com outra de posto baixo, objeto de estudo do meu projeto de doutorado. Através de conceitos básicos como posto e esparsidade matriciais, além de princípios de minimização de funções reais, entenderemos uma das maneiras de realizar a separação entre os objetos que se movem em um vídeo e seu plano de fundo, no contexto de sistemas de videovigilância.
Aluno: Melissa de Moraes Carvalho
Análise da generalização de modelo de deep learning criado ao se otimizar a função perda “Local Entropy” em comparação com funções de perda tradicionais (Cross Entropy) na tarefa de classificar imagens.
Comitê Científico

Christian da Silva Rodrigues
Concluiu graduação em Química pela Universidade Estadual de Campinas (2005) e obteve doutorado em Física Teórica pela University of Aberdeen (2010). Em seguida fez Pós-doutorado no Max Planck Institute for Mathematics in the Sciences, Alemanha, onde permaneceu como pesquisador associado até 2016. Retornou ao Brasil inicialmente com uma bolsa de pós-doutorado Fapesp, seguida de um Auxílio Jovem Pesquisador Fapesp, ambos no Instituto de Matemática, Estatística e Computação Científica da Universidade Estadual de Campinas. Em 2017 foi contratado no Departamento de Matemática Aplicada do mesmo instituto. Atualmente é professor doutor da Universidade Estadual de Campinas. Tem experiência na área de Matemática, com ênfase em Sistemas Dinâmicos, Teoria Ergódica, Probabilidade e Geometria. No momento, coordena o grupo de Análise Aplicada (CNPq).

Carlile Campos Lavor
Carlile Lavor é Prof. Titular, desde 2015, do Instituto de Matemática, Estatística e Computação Científica (IMECC - UNICAMP), com graduação em Matemática pela Universidade Estadual de Campinas (UNICAMP, 1996), doutorado em Computação pela Universidade Federal do Rio de Janeiro (COPPE - UFRJ, 2001), pós-doutorado em Computação Quântica pelo Laboratório Nacional de Computação Científica (LNCC, 2003) e livre-docência em Combinatória pela Universidade Estadual de Campinas (UNICAMP, 2006). Entre 2012 e 2013, foi Chefe do Dep. de Matemática Aplicada (IMECC - UNICAMP), e entre 2015 e 2016, foi Diretor Associado do IMECC. No biênio 2018-2019, foi Presidente da Sociedade Brasileira de Matemática Aplicada e Computacional (SBMAC) e, em 2021, recebeu o PRÊMIO ELON LAGES LIMA, juntamente com L.A.F. Fernandes (UFF) e M.M. Oliveira (UFRGS).

Maicon Ribeiro Correa
Professor Associado do Departamento de Matemática Aplicada da Unicamp, possui Gradução em Engenharia Civil pela Universidade Federal de Juiz de Fora (2001), Doutorado em Ciências em Modelagem Computacional pelo Laboratório Nacional de Computação Científica (2006), Pós Doutorados no Laboratório Nacional de Computação Científica (2007-2009) e na University of Texas at Austin (2015) e Título de Livre-Docência em Análise Numérica pela Unicamp (2019). Tem experiência em Modelagem Computacional e Análise Numérica, atuando principalmente nos seguintes temas: Métodos de Elementos Finitos Mistos/Híbridos Estabilizados, Esquemas Centrais para Leis de Conservação Hiperbólicas e Modelagem Numérica de Escoamentos em Meios Porosos. Atualmente é membro titular do Comitê de Assessoramento de Matemática e Estatística do CNPq, CA-MA.
Patrocinadores

Unisoma
Unisoma é uma empresa especializada em soluções de suprimentos, atuando no mercado a mais de 35 anos com excelência

Linear
A Linear é provedora de soluções matemático-computacionais para a otimização de processos e o aprimoramento digital da gestão empresarial. Com foco em promover o planejamento integrado dos diversos elos da cadeia de suprimentos, desenvolve ferramentas e soluções sob medida para cada cliente.

Routeasy
Routeasy é uma empresa especializada em software de roteirização, diminuindo os gastos com transportes de diversas empresas
Apoio





Camisetas
- Ocorreu uma remodelagem da camiseta, além de uma nova cor ter sido adicionada à paleta

