Abstract

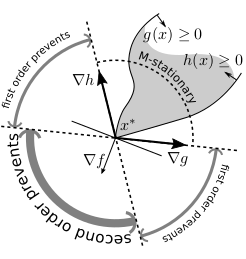
Mathematical programs with complementarity constraints (MPCCs) are difficult optimization problems that do not satisfy the majority of the usual constraint qualifications (CQs) for standard nonlinear optimization. Despite this fact, classical methods behave well when applied to MPCCs. Recently, Izmailov, Solodov, and Uskov proved that first order augmented Lagrangian methods, under a natural adaption of the linear independence constraint qualification to the MPCC setting (MPCC-LICQ), converge to strongly stationary (S-stationary) points, if the multiplier sequence is bounded. If the multiplier sequence is not bounded, only Clarke stationary (C-stationary) points are recovered. In this paper we improve this result in two ways. For the case of bounded multipliers we are able replace the MPCC-LICQ assumption by the much weaker MPCC-relaxed positive linear dependence condition (MPCC-RCLPD). For the case with unbounded multipliers, building upon results from Scholtes, Anitescu, and others, we show that a second order augmented Lagrangian method converges to points that are at least Mordukhovich stationary (M-stationary) but we still need the more stringent MPCC-LICQ assumption. Numerical tests, validating the theory, are also presented.