Abstract

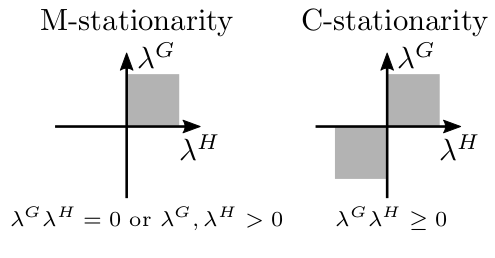
In recent years, the theoretical convergence of iterative methods for solving nonlinear constrained optimization problems has been addressed using sequential optimality conditions, which are satisfied by minimizers independently of constraint qualifications (CQs). Even though there is a considerable literature devoted to sequential conditions for standard nonlinear optimization, the same is not true for mathematical programs with complementarity constraints (MPCCs). In this paper, we show that the established sequential optimality conditions are not suitable for the analysis of convergence of algorithms for MPCC. We then propose new sequential optimality conditions for usual stationarity concepts for MPCC, namely, weak, Clarke, and Mordukhovich stationarity. We call these conditions AW-, AC-, and AM-stationarity, respectively. The weakest MPCC-tailored CQs associated with them are also provided. We show that some of the existing methods for MPCC reach AC-stationary points, extending previous convergence results. In particular, the new results include the linear case, not previously covered.