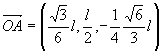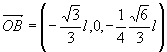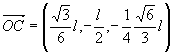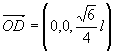
|
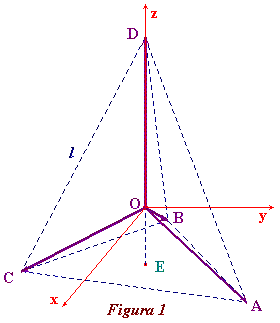
Exercício: Molécula de metano. As moléculas de metano (CH4) têm o formato de um tetraedro regular,
com um átomo de hidrogênio em cada vértice, cada um deles ligado
ao átomo de carbono no centro do tetraedro. Essas ligações são representadas, na figura 1, pelos vetores OA, OB, OC e OD.
Mostre que a soma desses vetores é o vetor nulo e calcule o ângulo formado por duas ligações. |
|
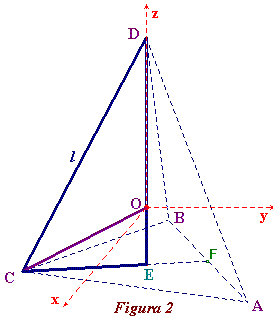
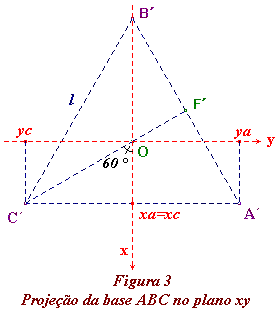
Como o segmento CF é a altura do triângulo equilátero CAB, isto é, a altura do triângulo base do tetraedro, temos que CE é igual a dois terços da altura CF.
Portanto, 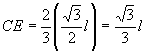 A seguir, utilizando o Teorema de Pitágoras e os triângulos retângulos CED e CEO, obtemos  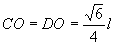 |
|
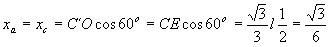  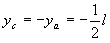
|
|
Agora vamos calcular o ângulo entre duas ligações. Para isto, basta calcular o ângulo entre os vetores OA e OB. 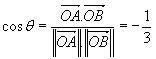 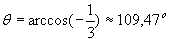 |