Respostas do exercícios ímpares
Livro “NOTAS DE GEOMETRIA ANALÍTICA”
(José Mario Martinez)
1- Sugest.: Use a definição de produto escalar
![]()
3- (2.2): Sugest.: Tente manipular a tese até chegar numa verdade e depois volte seus passos. Prove para o caso em que n = 2 e depois expanda para n qualquer;
(2.3): Sugest.: Aproveitando-se do resultado em (2.2) tente desenvolver usando:
(i) ||x|| = ||x - y + y|| e (ii) ||y|| = ||y – x + x|| e lembre que ||x - y|| = || y – x|| ;
(2.4): Sugest.: Aproveitando-se do resultado em (2.2) faça as
substituições u = x - y e v = y - z;
(2.5): Sugest.: Desenvolva ||x+y||2 e lembre que <x,y> = 0 quando x e y são ortogonais.
5- Sugest.: Refaça no caderno o desenvolvimento que segue o corolário 2.2 (livro pgs 19 e 20).
7- Sugest.: Use o fato de que sistemas lineares homogêneos são da forma AX = 0, e lembre também de que o produto de matrizes é distributivo (desde que sejam satisfeitas as condições para multiplicação de matrizes!).
9- Sugest.: Desenvolva a igualdade e verifique que ela só vai ser verdadeira se <v,w> = 0, ou seja, se v e w forem ortogonais.
11- Tente desenhar uma reta qualquer e um ponto Q fora da reta. Note que um ponto P “livre” na reta pode fornecer um vetor (P-Q) tão grande quanto se desejar, bastando caminhar com P ao longo da reta, mas, quando (P-Q) for ortogonal, a distância será a menor.
13.Dist = ![]() ,
,  e
e 
15- Use uma idéia similar ao do exercício 11, fixando um ponto da reta L1 e o interpretando como o ponto que está fora da reta L2.
17- dist =![]() e
e 
19- Precisa da lista do capítulo 1!!!
21- ![]() Vetor normal:
Vetor normal: ![]() Vetor diretor:
Vetor diretor: ![]() .
.
23-  Vetores normais:
Vetores normais: 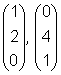 Vetor diretor:
Vetor diretor: ![]() .
.
25- ![]() Vetor normal:
Vetor normal: ![]() Vetor diretor:
Vetor diretor: ![]() .
.
27.  Vetores normais:
Vetores normais:  Vetor diretor:
Vetor diretor: ![]()
29 
31- Esta é a versão no Rn para o exercício 15, lembrando que uma reta é uma variedade afim de dimensão 1.
33- Tente mostrar que ![]() e
e ![]() usando a definição de
combinação linear, tanto no teorema quanto no corolário.
usando a definição de
combinação linear, tanto no teorema quanto no corolário.