Olá, Luiz Felipe.
A integral que aparece no exemplo 5, já na página 1024 ...é chata, mas muito importante para a cultura geral de um estudante que faz exatas, vale o sacrifício, se você não souber da história por trás do tal exemplo 5, uma tribo nerd de outras universidades vai rir de você, dizer que aqui em Campinas a Unicamp fica na terra que o boi falou etc., dirão que somos caipiras, os professores da USP, se souberem, vão rir de mim, vai ser uma tragédia.
Vamos conversar sobre ela, que será, com as manobras das páginas 1024 e 1025, resolvida com integrais duplas e coordenadas polares, como vou tentar explicar em detalhes neste email.
parte1: Apenas observações. A importância da tal integral para a definição da Erf e das distribuições gaussianas.
Primeiro, a tal integral é definida com limites infinitos mesmo,
I = Integrate[Exp[-x^2], {x, 0, infinito}],
é aquilo que chamamos de integral imprópria. A matemática torna precisas as integrais impróprias empregando limites, define a integral acima como o limite, quando b tende a infinito, da integral
I(b) = Integrate[Exp[-x^2], {x, 0, b}].
Esta integral existe, pois a teoria garante que existe sempre a integral de uma função contínua num intervalo.
Porém, pode-se mostrar que a função I(b) da variável b, definida por esta integral não pode ser escrita com as funções que, até um certo momento, existiam no vocabulário humano ...funções como potências, senos, exponenciais.
Como esta integral é muito útil no estudo de probabilidades, aparecia a todo momento, resolveram definir uma nova função no tal vocabulário, definiram
Erf(b) = 2/((pi)^(1/2)) Integrate[Exp[-x^2], {x, 0, b}],
veja na primeira foto anexa, no help do mathematica a definição de Erf ...sempre use o help quando aparecer alguma função que não conhece, é muito fácil de usar, basta clicar no menu HELP e digitar Erf ...e lá, em Details, você acha a definição desta função, que está implantada no mathematica. Também acha algumas de suas propriedades ...se procurar no google também achará muita coisa sobre a Erf, cujo nome é Error Function.
O fator numérico, que é o inverso da metade da raiz de pi é escolhido de forma que Erf(b) tenda a um quando b tende a infinito. Este lance de tender a um é para facilitar as aplicações em estatística. A distribuição normal de Gauss é uma espécie de distribuição que é um limite de muitas outras na estatística. Sua integral pode ser escrita facilmente a partir da Erf, dê uma pesquisada no assunto, vale a pena. Da mesma forma que seno e cosseno são úteis por vários motivos, inclusive por facilitarem descrevermos o movimento harmônico, a Erf, é útil, entre outros por facilitar o cálculo de probabilidades. A Erf muitas vezes está associada a curva de crescimento, ou acumulo de um fator aleatório, que é regido pela gaussiana (contágio por vírus talvez, em certas situações e teatros fixos, seja um exemplo)>
Se tem algum interesse por estatística, há um livro muito interessante, bem prático, não tão acadêmico, chamado de 'O Andar do Bêbado', de Mlodinow, que como comentado no texto da lista 2, pode ser baixado de
http://93.174.95.29/main/7E14539BC4290C2E5AB9DE99F53320D0
...bem, no exemplo 5 o texto do Edwards e Penney os autores estão explicando qual é o motivo do tal inverso da metade de raiz de pi na definição da Erf. Isto se deve ao fato de que a integral I, com a qual começamos este texto, dá exatamente a metade da raiz de pi.
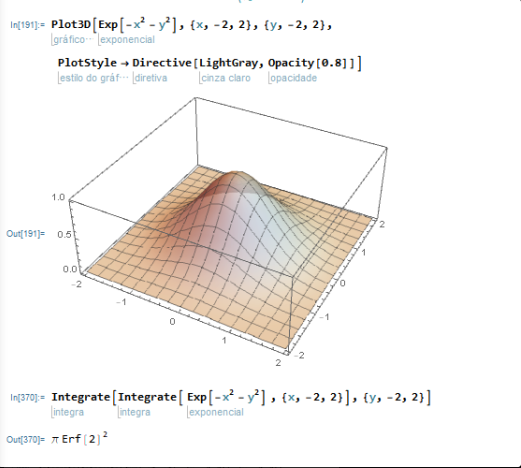
No notebook, fazemos algumas continhas com a Erf, a integral procurada etc., para mostrar a vocês. Os seus desenhos, dos gráficos de Exp[-(x^2+y^2)] sobre um círculo e um quadrado estão muito legais.
parte2: como a integral imprópria I é calculada por meio de integrais duplas em polares.
O exemplo 5 explica como as integrais duplas e as coordenadas polares podem ser utilizadas para ver que a imprópria I dá metade de pi.
A conversa é longa, primeiro notamos que, haja vista que Exp[-x^2] é função par, temos que
2 I(b) = Integrate[Exp[-x^2], {x, -b, b}],
trocar x por y numa integral definida não altera seu valor, portanto
2 I(b) = Integrate[Exp[-y^2], {y, -b, b}],
daí
(2I(b))^2 = Integrate[Exp[-x^2], {x, -b, b}] vezes Integrate[Exp[-y^2], {y, -b, b}] (*)
mas isto implica numa igualdade de (2I(b))^2 com uma integral dupla num quadrado.
A integral que aparece no exemplo 5, já na página 1024 ...é chata, mas muito importante para a cultura geral de um estudante que faz exatas, vale o sacrifício, se você não souber da história por trás do tal exemplo 5, uma tribo nerd de outras universidades vai rir de você, dizer que aqui em Campinas a Unicamp fica na terra que o boi falou etc., dirão que somos caipiras, os professores da USP, se souberem, vão rir de mim, vai ser uma tragédia.
Vamos conversar sobre ela, que será, com as manobras das páginas 1024 e 1025, resolvida com integrais duplas e coordenadas polares, como vou tentar explicar em detalhes neste email.
parte1: Apenas observações. A importância da tal integral para a definição da Erf e das distribuições gaussianas.
Primeiro, a tal integral é definida com limites infinitos mesmo,
I = Integrate[Exp[-x^2], {x, 0, infinito}],
é aquilo que chamamos de integral imprópria. A matemática torna precisas as integrais impróprias empregando limites, define a integral acima como o limite, quando b tende a infinito, da integral
I(b) = Integrate[Exp[-x^2], {x, 0, b}].
Esta integral existe, pois a teoria garante que existe sempre a integral de uma função contínua num intervalo.
Porém, pode-se mostrar que a função I(b) da variável b, definida por esta integral não pode ser escrita com as funções que, até um certo momento, existiam no vocabulário humano ...funções como potências, senos, exponenciais.
Como esta integral é muito útil no estudo de probabilidades, aparecia a todo momento, resolveram definir uma nova função no tal vocabulário, definiram
Erf(b) = 2/((pi)^(1/2)) Integrate[Exp[-x^2], {x, 0, b}],
veja na primeira foto anexa, no help do mathematica a definição de Erf ...sempre use o help quando aparecer alguma função que não conhece, é muito fácil de usar, basta clicar no menu HELP e digitar Erf ...e lá, em Details, você acha a definição desta função, que está implantada no mathematica. Também acha algumas de suas propriedades ...se procurar no google também achará muita coisa sobre a Erf, cujo nome é Error Function.
O fator numérico, que é o inverso da metade da raiz de pi é escolhido de forma que Erf(b) tenda a um quando b tende a infinito. Este lance de tender a um é para facilitar as aplicações em estatística. A distribuição normal de Gauss é uma espécie de distribuição que é um limite de muitas outras na estatística. Sua integral pode ser escrita facilmente a partir da Erf, dê uma pesquisada no assunto, vale a pena. Da mesma forma que seno e cosseno são úteis por vários motivos, inclusive por facilitarem descrevermos o movimento harmônico, a Erf, é útil, entre outros por facilitar o cálculo de probabilidades. A Erf muitas vezes está associada a curva de crescimento, ou acumulo de um fator aleatório, que é regido pela gaussiana (contágio por vírus talvez, em certas situações e teatros fixos, seja um exemplo)>
Se tem algum interesse por estatística, há um livro muito interessante, bem prático, não tão acadêmico, chamado de 'O Andar do Bêbado', de Mlodinow, que como comentado no texto da lista 2, pode ser baixado de
http://93.174.95.29/main/
...bem, no exemplo 5 o texto do Edwards e Penney os autores estão explicando qual é o motivo do tal inverso da metade de raiz de pi na definição da Erf. Isto se deve ao fato de que a integral I, com a qual começamos este texto, dá exatamente a metade da raiz de pi.
No notebook, fazemos algumas continhas com a Erf, a integral procurada etc., para mostrar a vocês. Os seus desenhos, dos gráficos de Exp[-(x^2+y^2)] sobre um círculo e um quadrado estão muito legais.
parte2: como a integral imprópria I é calculada por meio de integrais duplas em polares.
O exemplo 5 explica como as integrais duplas e as coordenadas polares podem ser utilizadas para ver que a imprópria I dá metade de pi.
A conversa é longa, primeiro notamos que, haja vista que Exp[-x^2] é função par, temos que
2 I(b) = Integrate[Exp[-x^2], {x, -b, b}],
trocar x por y numa integral definida não altera seu valor, portanto
2 I(b) = Integrate[Exp[-y^2], {y, -b, b}],
daí
(2I(b))^2 = Integrate[Exp[-x^2], {x, -b, b}] vezes Integrate[Exp[-y^2], {y, -b, b}] (*)
mas isto implica numa igualdade de (2I(b))^2 com uma integral dupla num quadrado.
Vamos explicar seja e integral dupla dada por
Integrate[Integrate[Exp[-(x^2 + y^2)], {x,-b,b}], {y,-b,b}],
pois na hora de fazer a integral dupla acima no quadrado de lado b, podemo utilizar a propriedade da exponencial para quebrá-la num produto,
Integrate[Integrate[Exp[-x^2] Exp[-y^2], {x,-b,b}], {y,-b,b}],
lembrar que na primeira integral y é constante e podemos deixar a 'constante Exp[-y^2]' de fora da integral em x, obtendo
Integrate[Exp[-y^2] Integrate[Exp[-x^2], {x,-b,b}], {y,-b,b}],
e daí lembrar que Integrate[Exp[-x^2],{x,-b,b}] não depende de y, e podemos deixá-lo de fora da integral em y, daí obtemos a expressão (*), para (2I(b))^2, mais acima.
Integrate[Integrate[Exp[-(x^2 + y^2)], {x,-b,b}], {y,-b,b}],
pois na hora de fazer a integral dupla acima no quadrado de lado b, podemo utilizar a propriedade da exponencial para quebrá-la num produto,
Integrate[Integrate[Exp[-x^2] Exp[-y^2], {x,-b,b}], {y,-b,b}],
lembrar que na primeira integral y é constante e podemos deixar a 'constante Exp[-y^2]' de fora da integral em x, obtendo
Integrate[Exp[-y^2] Integrate[Exp[-x^2], {x,-b,b}], {y,-b,b}],
e daí lembrar que Integrate[Exp[-x^2],{x,-b,b}] não depende de y, e podemos deixá-lo de fora da integral em y, daí obtemos a expressão (*), para (2I(b))^2, mais acima.
Bem será fácil obtermos I(b) se conseguirmos calcular
(2I(b))^2 = Integrate[Integrate[Exp[-(x^2 + y^2)], {x,-b,b}], {y,-b,b}]
que é uma integral dupla num quadrado de lado b, que representaria o volume embaixo do gráfico de
z = Exp[-(x^2 + y^2)
e acima do tal quadrado, centrado no plano xy dado por z = 0, vamos obter o limite de I(b), quando b vai para infinito ...e verificar que dá a metade da raiz de pi.
Agora faremos algumas observações, as quais levarão a conclusão de que,
se estamos interessados no limite, podemos fazer esta integral num
círculo, em polares, que é mais fácil.
Notamos primeiro que o tal quadrado de lado 2b, centrado na origem, com lados paralelos aos eixos x e y, pode ser inscrito num círculo centrado na origem, de raio dado por b(2^(1/2)). Assim, se calculássemos o volume acima deste círculo de raio b(2^(1/2)) e abaixo do tal gráfico, isto daria maior que I(b).
Por outro lado, existe um círculo inscrito no tal quadrado, o círculo de raio b, com centro na origem. Assim, se calculássemos o volume acima deste círculo de raio b e abaixo do tal gráfico, isto daria menor que I(b).
Oras, se mandamos b para infinito, daí não faz diferença se o volume está acima de um círculo de raio b ou b(2^(1/2)), os dois limites vão para o mesmo valor e pelo teorema do sanduíche, o limite, quando b vai para infinito, de (2I(b))^2 é igual ao limite, quando R vai para infinito, da integral de
z = Exp[-(x^2 + y^2)]
num círculo de raio R centrado na origem.
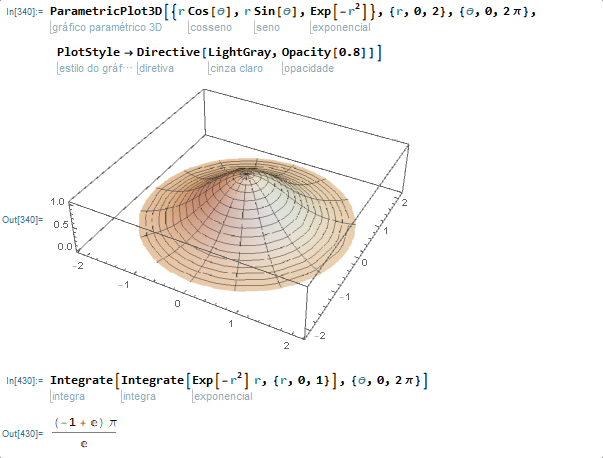
A tal integral, no círculo, pode ser feita em polares, assim sendo I é o limite, quando R vai para infinito de
Ipol(R) = Integrate[Integrate[Exp[-r^2] r, {theta, 0, 2pi}], {r,0,R}]
...note que, ao passarmos para polares, trocamos x por costheta e y por sentheta, daí x^2+y^2 vira r^2 pela relação fundamental. Além de fazermos a troca de variáveis, devemos multiplicar o integrando pelo fator de correção r.
Bem, a primeira integral, em theta, com r fixo, é fácil de fazer, pois não há dependência em theta e integrar em theta apenas multiplica o integrando por 2pi, ficamos com a segunda integral,
Ipol(R) = Integrate[2pi Exp[-r^2] r, {r,0,R}]
que agora é feita em r, variando entre 0 e o raio R do círculo ...e acontece um lance de sorte!!! ...aquele r da correção, no integrando, que escrevemos da forma clássica,
2pi Exp[-r^2] rdr
...está encostadinho no dr, sugere uma troca de variáveis,
u = r^2, du = 2rdr, 2piExp[-r^2]rdr = pi Exp[-u]du,
a integral da exponencial é ela mesma, aqui tem o sinal e uma primitiva para esta integração é
-pi Exp[-u] = -pi Exp[-r^2].
Assim sendo
Ipol(R) = Integrate[2pi Exp[-r^2] r, {r,0,R}] =
= -pi Exp[-R^2] - (-pi Exp[0^2]) = pi(1 - Exp[-R^2]),
quando R tende a infinito, Ipol(R) tende a pi, portanto o limite de (2I(b))^2, que dá (2I)^2, é igual a pi, concluímos que I vale metade da raiz de pi.
Saudações Filosóficas. Márcio.
Notamos primeiro que o tal quadrado de lado 2b, centrado na origem, com lados paralelos aos eixos x e y, pode ser inscrito num círculo centrado na origem, de raio dado por b(2^(1/2)). Assim, se calculássemos o volume acima deste círculo de raio b(2^(1/2)) e abaixo do tal gráfico, isto daria maior que I(b).
Por outro lado, existe um círculo inscrito no tal quadrado, o círculo de raio b, com centro na origem. Assim, se calculássemos o volume acima deste círculo de raio b e abaixo do tal gráfico, isto daria menor que I(b).
Oras, se mandamos b para infinito, daí não faz diferença se o volume está acima de um círculo de raio b ou b(2^(1/2)), os dois limites vão para o mesmo valor e pelo teorema do sanduíche, o limite, quando b vai para infinito, de (2I(b))^2 é igual ao limite, quando R vai para infinito, da integral de
z = Exp[-(x^2 + y^2)]
num círculo de raio R centrado na origem.
A tal integral, no círculo, pode ser feita em polares, assim sendo I é o limite, quando R vai para infinito de
Ipol(R) = Integrate[Integrate[Exp[-r^2] r, {theta, 0, 2pi}], {r,0,R}]
...note que, ao passarmos para polares, trocamos x por costheta e y por sentheta, daí x^2+y^2 vira r^2 pela relação fundamental. Além de fazermos a troca de variáveis, devemos multiplicar o integrando pelo fator de correção r.
Bem, a primeira integral, em theta, com r fixo, é fácil de fazer, pois não há dependência em theta e integrar em theta apenas multiplica o integrando por 2pi, ficamos com a segunda integral,
Ipol(R) = Integrate[2pi Exp[-r^2] r, {r,0,R}]
que agora é feita em r, variando entre 0 e o raio R do círculo ...e acontece um lance de sorte!!! ...aquele r da correção, no integrando, que escrevemos da forma clássica,
2pi Exp[-r^2] rdr
...está encostadinho no dr, sugere uma troca de variáveis,
u = r^2, du = 2rdr, 2piExp[-r^2]rdr = pi Exp[-u]du,
a integral da exponencial é ela mesma, aqui tem o sinal e uma primitiva para esta integração é
-pi Exp[-u] = -pi Exp[-r^2].
Assim sendo
Ipol(R) = Integrate[2pi Exp[-r^2] r, {r,0,R}] =
= -pi Exp[-R^2] - (-pi Exp[0^2]) = pi(1 - Exp[-R^2]),
quando R tende a infinito, Ipol(R) tende a pi, portanto o limite de (2I(b))^2, que dá (2I)^2, é igual a pi, concluímos que I vale metade da raiz de pi.
Saudações Filosóficas. Márcio.