Olá, Lucca.
Parabéns pela excelente pergunta, está chegando a pontos avançados nosso
curso está decolando,
igual à pandemia (trocadilho meio sem graça, né?).
Seu note vai anexo, com reformas e as seguintes considerações,
que permitirão entendê-lo melhor:
No caso desses exercícios, as duas superfícies naturalmente fecham uma
região.
Daí a região do plano xy onde fazemos a integral dupla é a sombra da
região,
i. no caso do 33, quando as duas superfícies se encontram temos
25 - x^2 - y^2 = 0, assim percebemos que a sombra é o círculo
interior à circunferência x^2 + y^2 = 25.
A região existe apenas sobre este círculo. Para fatiar na direção x, fixamos x.
i. no caso do 33, quando as duas superfícies se encontram temos
25 - x^2 - y^2 = 0, assim percebemos que a sombra é o círculo
interior à circunferência x^2 + y^2 = 25.
A região existe apenas sobre este círculo. Para fatiar na direção x, fixamos x.
Daí y varia de -(25-x^2)^(1/2) até (25+x^2)^(1/2), na fatia em que x é
fixo.
Para obter a área da fatia devemos integrar a diferença de alturas,
(25 - x^2 -y^2) - 0, em y, entre estes dois extremos que dependem de x,
A(x) = Integrate[25 - x^2 - y^2, {y, -(25-x^2)^(1/2), (25+x^2)^(1/2)}]
...isto dá a área da fatia móvel. Alterei seu primeiro desenho e desenhei a fatia no
caso em que x é fixo e igual a 3, daí y varia de -4 a 4. Note que nesta fatia,
pondo x=3 e y=4t, com t entre -1 e 1, temos
zcima = 25 - x^2 -y^2 = 25 - 9 -16t^2.
Para obter a área da fatia devemos integrar a diferença de alturas,
(25 - x^2 -y^2) - 0, em y, entre estes dois extremos que dependem de x,
A(x) = Integrate[25 - x^2 - y^2, {y, -(25-x^2)^(1/2), (25+x^2)^(1/2)}]
...isto dá a área da fatia móvel. Alterei seu primeiro desenho e desenhei a fatia no
caso em que x é fixo e igual a 3, daí y varia de -4 a 4. Note que nesta fatia,
pondo x=3 e y=4t, com t entre -1 e 1, temos
zcima = 25 - x^2 -y^2 = 25 - 9 -16t^2.

Tendo A(x), basta integrá-la em x, de -5 a 5. Temos ao final a dupla
Integrate[Integrate[25-x^2-y^
estas integrais são chatas de fazer, com coordenadas polares ficariam muito
fáceis, veremos isto no próximo tópico. Por enquanto, fazemos no soft,
fiz a conta no seu notebook reformado, deu 625pi/2.
ii. no caso do 34, quando as superfícies se encontram temos
x^2 + 2y^2 = 12 - 2x^2 - y^2
assim percebemos que a sombra é o círculo x^2 + y^2 = 4.
A região existe apenas sobre este círculo. Para fatiar na direção x,
fixamos x. Daí y varia de -(4-x^2)^(1/2) até (4+x^2)^(1/2), na fatia em
que x é fixo.
Para obter a área da fatia devemos integrar a diferença de alturas,
(12 - 2x^2 - y^2) - (x^2 + 2y^2) = 12 - 3x^2 - 3y^2, em y,
entre estes dois extremos que dependem de x,
A(x) = Integrate[12 - 3x^2 - 3y^2, {y, -(4-x^2)^(1/2), (4-x^2)^(1/2)}]
...isto dá a área da fatia móvel. Alterei seu primeiro desenho e desenhei a fatia no
caso em que x é fixo e igual a 2^(1/2), daí y varia de -2^(1/2) a 2^(1/2).
Note que nesta fatia, pondo x=2^(1/2), e y=2^(1/2)t, com t de -1 a 1,
zcima = 12 - 2x^2 - y^2 = 12 - 4 - 2t^2 = 8 - t^2
zbaixo = x^2 + 2y^2 = 2 + 4t^2.
Também coloquei a sombra, adicionando a função identicamente nula no seu Plot3D
e dei um jeito de fazer aparecer a sombra da fatia no círculo.
Para obter a área da fatia devemos integrar a diferença de alturas,
(12 - 2x^2 - y^2) - (x^2 + 2y^2) = 12 - 3x^2 - 3y^2, em y,
entre estes dois extremos que dependem de x,
A(x) = Integrate[12 - 3x^2 - 3y^2, {y, -(4-x^2)^(1/2), (4-x^2)^(1/2)}]
...isto dá a área da fatia móvel. Alterei seu primeiro desenho e desenhei a fatia no
caso em que x é fixo e igual a 2^(1/2), daí y varia de -2^(1/2) a 2^(1/2).
Note que nesta fatia, pondo x=2^(1/2), e y=2^(1/2)t, com t de -1 a 1,
zcima = 12 - 2x^2 - y^2 = 12 - 4 - 2t^2 = 8 - t^2
zbaixo = x^2 + 2y^2 = 2 + 4t^2.
Também coloquei a sombra, adicionando a função identicamente nula no seu Plot3D
e dei um jeito de fazer aparecer a sombra da fatia no círculo.
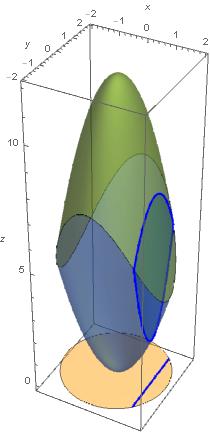
Tendo A(x), área da fatia para cada corte x fixo,
basta integrá-la em x, de -2 a 2. Temos
Integrate[Integrate[12 - 3x^2 - 3y^2, {y,-(4-x^2)^(1/2),(4+x^2)^(1/
estas integrais são chatas de fazer, com coordenadas polares ficariam muito
fáceis, veremos isto no próximo tópico. Por enquanto, fazemos no soft,
fiz a conta no seu notebook reformado, deu 24pi.
iii. no caso do 36 quando as superfícies se encontram temos
x^2 + 3y^2 = 4 - y^2
assim percebemos que a sombra é o a elipse (x/2)^2 + y^2 = 1.
A região existe apenas sobre esta elipse, com semi-eixo maior na
horizontal, igual a 2^(1/2) e semi-eixo menor na vertical, igual a 1.
Para fatiar na direção x, fixamos x. Daí y varia de
-(1-(x/2)^2)^(1/2) até (1-(x/2)^2)^(1/2), na fatia em que x é fixo.
Para obter a área da fatia devemos integrar a diferença de alturas,
(4 - y^2) - (x^2 + 3y^2) = 4 -x^2 -4y^2, em y,
entre estes dois extremos que dependem de x,
A(x) = Integrate[4 -x^2 -4y^2, {y, -(1-(x/2)^2)^(1/2), (1-(x/2)^2)^(1/2)}]
...isto dá a área da fatia móvel. Alterei seu primeiro desenho e desenhei a fatia no
caso em que x é fixo e igual a 1, daí y varia de -3^(1/2)/2 a 3^(1/2)/2.
Note que nesta fatia, pondo x=1, y=3^(1/2)t/2, com t de -1 a 1, temos
zcima = 4 - y^2 = 4 - 3t^2/4
zbaixo = x^2 + 3y^2 = 1 + 9t^2/4.
Também coloquei a sombra, adicionando a função identicamente nula no seu Plot3D
e dei um jeito de fazer aparecer a sombra da fatia no círculo.
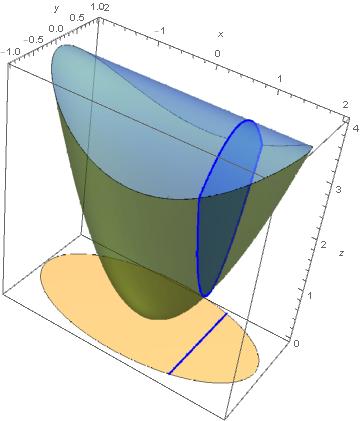
Tendo A(x), área da fatia para cada corte x fixo,
basta integrá-la em x, de -1 a 1. Temos
Integrate[Integrate[4 -x^2 -4y^2, {y, -(1-(x/2)^2)^(1/2), (1-(x/2)^2)^(1/2)}],{x,-1,1}]
estas integrais são chatas de fazer, com coordenadas polares elípticas
ficariam muito fáceis, veremos isto no próximo tópico. Por enquanto,
fazemos no soft, fiz a conta
no seu notebook reformado, deu 3(3)^1/2 + 4pi/3.
Abraço. Márcio.
